עצי החלטה

תקציר התאוריה

עצי החלטה הינם כלי נפוץ ופשוט יחסית לסיווג ורגרסיה. בבסיסו עץ החלטה הינו מימוש מסוים של פונקציות לוגיות (כניסה ויציאה דיסקרטית), אולם ניתן ליישמו גם עבור משתנים רציפים על ידי דיסקרטיזציה.

:דוגמא לשימוש בעץ החלטה לצורך סיווג פירות לפי מספר מאפיינים

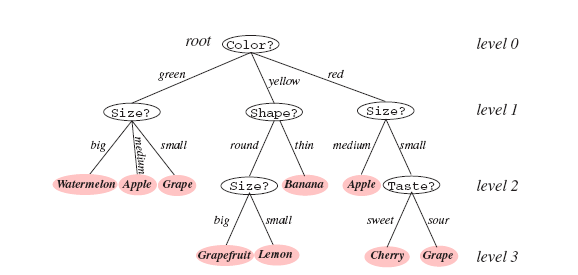
דוגמא לשימוש בעץ החלטה כאשר מרחק הקלט הוא רציף:

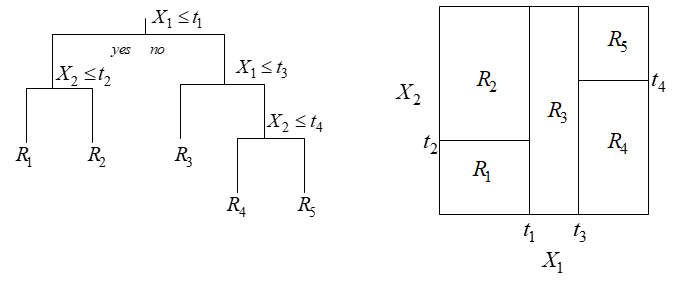
מטרת חלק זה היא להדגים בנייה של עץ החלטה, על סמך אוסף דוגמאות מתויג, כאשר נבנה את עץ ההחלטה עם התכונות הבאות:

1. סיווג נכון של מרבית הדוגמאות.
2. עץ קצר (פשוט) ככל הניתן.

תכונה 2 חשובה משתי סיבות:

1. פשטות המימוש.
2. יכולת הכללה: מניעת התאמת-יתר לאוסף הדוגמאות הנתון.

נציג מספר הגדרות ומספר קריטריונים שונים לבחירת המאפיין המיטבי שעל פיו נבנה העץ. יהי $D$ אוסף של $N$ דוגמאות מסווגות $D=\{x_i,y_i\}_{i=1}^N$, כך ש- $y_i \in \{1, \dots, K \}$ כאשר $K$ הינו מספר המחלקות האפשריות.

השכיחות היחסית (או “הפילוג האמפירי”) של כל אחד מהסיווגים האפשריים בקבוצת הדוגמאות נתונה ע”י:

$$\hat{p}_j = \frac{1}{N} \sum_{i=1}^N I\{y_i = j \}\,, \quad \forall j = 1,\cdots, K$$

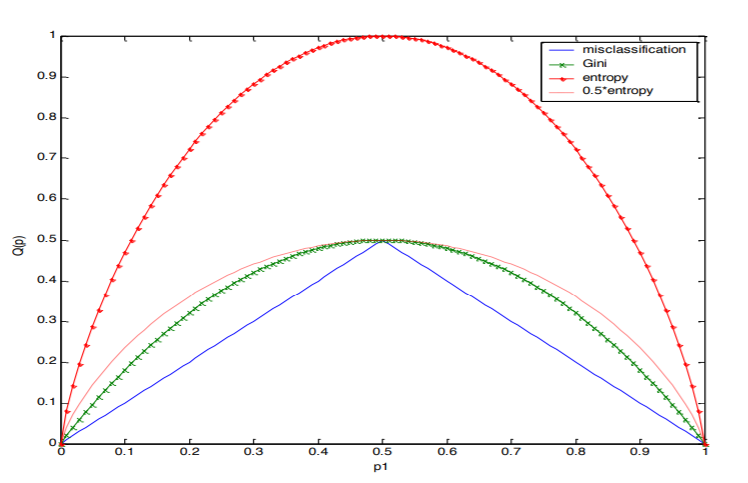
מדדים אחידות של $D$:

• שגיאת הסיווג:

$$Q(D) = 1 - \max_{j \in \{1, \dots, K \}} \hat{p}_j$$

• אינדקס Gini:

$$Q(D) = \sum_{j \in \{1, \dots, K \}} \hat{p}_j(1 - \hat{p}_j)$$

• אנטרופיה:

$$Q(D) = H(D) = \sum_{j \in \{1, \dots, K \}} \hat{p}_j \log \frac{1}{\hat{p}_j} = -\sum_{j \in \{1, \dots, K \}} \hat{p}_j \log {\hat{p}_j}$$

תכונות של $Q(D)$ :

1. $Q(D)=0$ עבור פילוג חד-ערכי ( $\hat{p}_j=1$ עבור $j$ כלשהו).
2. $Q(D)$ מקבל את ערכו המכסימלי עבור פילוג אחיד ($\hat{p}_j=\frac{1}{K}$ ).

תוספת המידע של מאפיין: נניח כי מאפיין $A$ כלשהו מחלק את $D$ למספר תת-קבוצות. נסמן תת-קבוצות אלו על ידי $\{D_m\,, m \in 1, \cdots, M\}$ , כאשר $M$ הינו אוסף הערכים האפשריים של $A$.

מדד האחידות המשוקלל עבור האוסף $\{D_m\}$ יוגדר עתה על ידי:

$$Q(D \lvert A) = \sum_{m=1}^M \frac{\lvert D_m \rvert }{N} Q(D_m)$$

כאשר $Q(D_m)$ הוא מדד לחוסר האחידות של תת-הקבוצה $D_m$.

מדד הטיב של המאפיין $A$ ביחס לקבוצת הדוגמאות $D$ יוגדר עתה על ידי

$$\Delta Q(D \lvert A) = Q(D) - Q(D \lvert A)$$

ניתן לראות כי זהו הגידול באחידות (או הקטנה בחוסר-האחידות) של האוסף $\{D_m\}$ לעומת קבוצת הדוגמאות המקורית $D$. כאשר $Q(\cdot)$ הינה האנטרופיה, $\Delta Q(D|A)$ נקרא גם תוספת המידע (information gain) של המאפיין $A$.

---

המאפיין $A$ שנבחר הוא (כעיקרון) זה שעבורו השיפור $\Delta Q(D \lvert A)$ הינו מקסימלי כלומר $Q(D \lvert A)$ מינימלי.

---

שאלה 12.1 – בניית עץ החלטה

בנה עץ החלטה המבוסס על קריטריון האנטרופיה, אשר בהינתן נתוני צבע שער, גובה, משקל, משתמש בקרם הגנה, קובע האם עתיד האדם להכוות מהשמש היוקדת.
סט דוגמאות הלימוד לצורך בניית העץ מוצג בטבלה הבאה:

פתרון שאלה 12.1

אנו נמצאים בשורש ולכן $D$ הוא קבוצת כל האנשים. ראשית נחשב את האנטרופיה על פני כלל הדוגמאות:

$$H(D) = -\frac{3}{8} \log{\frac{3}{8}} -\frac{5}{8} \log{\frac{5}{8}} = 0.954$$

כעת נבחן את האנטרופיה שתושרה לאחר פיצול לפי כל אחד מהמאפיינים האפשריים:

Hair:

ומדד הטיב של מאפיין Hair יחושב לפי האנטרופיה המשוקללת על פני הפיצולים האפשריים:

$$\Delta H(D \lvert Hair ) = H(S) -( \frac{1}{2} \cdot 1 + \frac{3}{8} \cdot 0 + \frac{1}{8} \cdot 0 ) = H(D) - \frac{1}{2}$$

Height:

ומדד הטיב של מאפיין Height יחושב לפי האנטרופיה המשוקללת על פני הפיצולים האפשריים:

$$\Delta H(D \lvert Height ) = H(S) -( \frac{3}{8} \cdot 0.918 + \frac{3}{8} \cdot 0.918 + \frac{2}{8} \cdot 0 ) = H(D) - 0.69$$

Weight:

ומדד הטיב של מאפיין weight יחושב לפי האנטרופיה המשוקללת על פני הפיצולים האפשריים:

$$\Delta H(D \lvert Weight ) = H(S) -( \frac{2}{8} \cdot 1 + \frac{3}{8} \cdot 0.918 + \frac{3}{8} \cdot 0.918 ) = H(D) - 0.9385$$

Lotion:

ומדד הטיב של מאפיין lotion יחושב לפי האנטרופיה המשוקללת על פני הפיצולים האפשריים:

$$\Delta H(D \lvert Lotion ) = H(S) -( \frac{5}{8} \cdot 0.97 + \frac{3}{8} \cdot 0 ) = H(D) - 0.606$$

מכאן שהמאפיין האופטימלי לפיצול הראשון (על פי קריטריון האנטרופיה) הוא Hair.

עבור הפיצול של הרמה השנייה נשים לב כי הענפים של Hair=brown ו Hair=red בעלי אנטרופיה מקסימלית. כלומר, ניתן לסווג את הדוגמאות בצורה מושלמת לכן אין צורך בפיצולים נוספים. לגבי הענף Hair=blonde: קבוצת הדוגמאות בענף זה היא:

פיצול לפי מאפיין height ייתן:

לפי weight:

לפי Lotion:

לפיכך הקריטריון האופטימלי (זה שממזער את קריטריון הגידול) הוא Lotion.

עץ ההחלטה הסופי יראה כך:

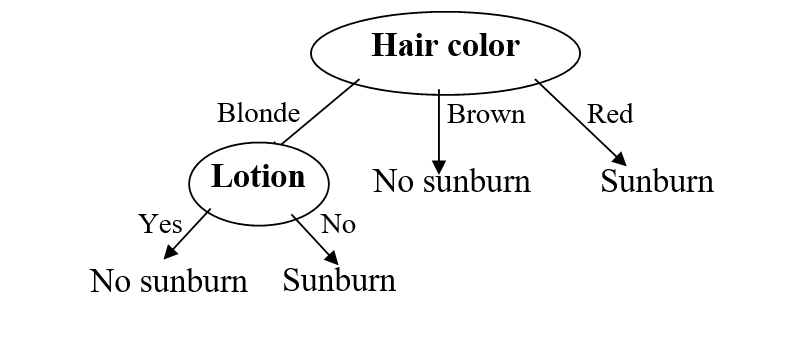
בעיית התאמת היתר (overfitting):

ניתן לסווג את הדוגמאות באופן מושלם רק על סמך “מאפיין” שם ו”מאפיין” זה בוודאי ייבחר בצומת הראשונה לפי קריטריון “תוספת המידע”. אולם לקריטריון זה ערך מועט לצורך חיזוי.

מקור הבעיה: בקריטריון שבו השתמשנו קיימת העדפה מובנית למאפיינים בעלי מספר ערכים רב.

פתרון אפשרי: נרמול “תוספת המידע” של מאפיין $A$ באופן הבא:

$$\Delta \widetilde{Q}(D \lvert A ) = \frac{\Delta Q(D \lvert A )}{\text{Split}(D , A)}$$

$\text{Split}(D , A)$ כאשר הינו מקדם פיצול מתאים. הגדרה מקובלת:

$$\text{Split}(D , A) = \log n(A)$$

$n(A)$ כאשר, היינו מספר הערכים השונים של הנאפיין $A$, המתקבלים על פני איברי הקבוצה $D$

מאפיינים רציפים:

נניח כי וקטור המאפיינים $x=(x_1,…,x_d )^T$ כולל רכיבים $x_j$ בעלי ערכים רציפים. במקרה זה, המבחן המקובל לגבי $x_j$ הינו מהצורה $x_j \leq t_j$. לפיכך, לבחירת המאפיין בכל צומת יש להוסיף את בחירת ערך הסף $t_j$.
עבור כל מבחן $A=\{ x_j \leq t_j \}$ ניתן להגדיר את תוספת המידע באופן הרגיל:

$$\Delta Q(S \lvert x_j,t_j )= \Delta Q(S \lvert A)$$

השלב הבא הוא מקסימיזציה על הסף $t_i$:

$$\Delta Q(S \lvert x_j ,t_j^* )= \max_{t_j} \Delta Q(S \lvert x_j, t_j)$$

ולאחר מכן בחירת המאפיין $x_j$ שעבורו מדד זה הינו מקסימלי.

Boosting - Adaboost

AdaBoost (Adaptive Boosting) הינה טכניקה לשיפור ביצועים של אלגוריתם סיווג על ידי שילוב ממושקל של מספר מסווגים. עיקרון מבוסס על בנייה איטרטיבית של מסווג אשר מורכב ממספר מסווגים, כשאר בתהליך הבנייה נשמר ווקטור של משקולות המעיד על טיב הסיווג של כל נקודה בסט על ידי סך הסיווגים הקודמים (מכל המסווגים). בכל שלב האלגוריתם מנסה לבנות מסווג שיתקן את הטעויות שנעשו מהמסווגים הקודמים.

נסמן:

• $N$ - גודל ה dataset
• $\left\lbrace\boldsymbol{x}_i,y_i\right\rbrace$ - המדידות והמחלקות.
• ערכי המחלקות הם $1,-1$

אלגוריתם:

• אתחל באופן אחיד את המשקולות עבור כל נקודה ב dataset: $D^{\left(t=0\right)}_i=\frac{1}{N}$
• המשך באופן איטרטיבי עבור אינדקס $t$ עד להגעת תנאי עצירה:
  1. בנה מסווג אופטימלי $h_t$ ביחס ל- dataset הממושקל
  2. חשב את שגיאת הסיווג של $h_t$ עבור ה dataset הממושקל: $\varepsilon=\sum_i D^t_iI\left\lbrace h\left(\boldsymbol{x}_i\right)\neq y_i\right\rbrace$
  3. חשב את משקל עבור המסווג $h_t$ לפי: $\alpha_t=\frac{1}{2}\ln\left(\frac{1-\varepsilon}{\varepsilon}\right)$
  4. עדכן את המשקולות עבור כל נקודה ב-dataset : $D^t_i=D^{t-1}_i\exp\left(-\alpha_ty_ih_t\left(\boldsymbol{x}_i\right)\right)$
  5. נרמל את המשקולות לפי: $Z=\sum_i D^t_i$ according to: $D^t_i=\frac{D^t_i}{Z}$

הסיווג הסופי נעשה על ידי קומבינציה לינארית של כל מסווגים והמשקל שלהם.

$$H\left(\boldsymbol{x}_i\right)=\text{sign}\left(\sum_t\alpha_th_t\left(\boldsymbol{x}_i\right)\right)$$

תרגיל 12.2: הדגמת האלגוריתם

נתבונן בבעיית סיווג חד מימדית עבור סט דוגמאות האימון:

$$\{(x_i,y_i)\}_{i=1}^3=\{(0,-1), (1,1), (2,-1) \}.$$

יהי המודל: $H\left(\boldsymbol{x}_i\right)=\text{sign}\left(\sum_t\alpha_th_t\left(\boldsymbol{x}_i\right)\right)$

1. האם קיימים מסווגים ליניאריים $\{h_t\}$ ופרמטרים $\{\alpha_t\}$ כך שהשגיאה של היפותזה $H(x)$ היא אפס על כל סט האימון? אם כן, מה ה-T המינימאלי לקבל שגיאה אפס?

2. רשום את שלבי אלגוריתם AdaBoost עבור הדוגמא.

פתרון

1. ראשית נסתכל בבעיה:

נשים לב, שמסווג בודד לא יפתור את הבעיה משום שלא קיימת הפרדה לינארית בין המחלקות. עבור שני מסווגים לא ניתן למצוא מקדמים $\alpha_t$ שעבור נקבל שגיאת אימון אפס. ניתן לקבל שגיאה אפס עבור שלושה מסווגים חלשים בהן נתייג נכון את כל הדוגמאות.

2. נאתחל את הפילוג:

$$D_1=\frac{1}{3}$$

נקח את המסווג הבא: $h_1 (x_i )=\{-1,-1,-1\}$

עבורו נקבל:

$$\epsilon_1=P_{D_1} (h_1 (x_i ) \neq y_i ) = \frac{1}{3} \\ a_1= \frac{1}{2} \log \frac{1 - \epsilon_1}{\epsilon_1} = 0.3466$$

וכרגע ניתן לעדכן את התפלגות הדוגמאות:

$$Z_1= \sum_i D_1 (i) \cdot \exp (-a_1 y_i h_1 (x_i )) \\ D_2 (i) = D_1 \cdot \frac{\exp(-a_1 y_i h_1 (x_i ))}{Z_1} = \{0.25,0.5,0.25\}$$

באיטרציה הבאה נבחר את המסווג הבא:

$$h_2 (x_i )=\{-1,+1,+1\}$$

עבורו נקבל:

$$\epsilon_2=P_{D_2} (h_2 (x_i ) \neq y_i ) = 0.25 \\ a_2 = \frac{1}{2} \log \frac{1-\epsilon_2}{\epsilon_2} = 0.5493$$

נעדכן את הפילוג לפי המסווג הנוסף:

$$Z_2 = \sum_i D_2 (i) \cdot \exp (-a_2 y_i h_2 (x_i )) \\ D_3(i) = D_2 \cdot \frac{\exp (-a_2 y_i h_2 (x_i ))}{Z_2} = \{0.1667,0.333,0.5\}$$

עבור הבעיה בדוגמה, מספיק עוד מסווג חלש אחד אותו נבחר כך:

$$h_3 (x_i )=\{+1,+1,-1\}$$

עבורו נקבל:

$$\epsilon_3=P_(D_3 ) (h_3 (x_i ) \neq y_i ) = 0.1667 \\ a_3 = \frac{1}{2} \log \frac{1-ϵ_3}{ϵ_3} = 0.8047$$

נעדכן את הפילוג לפי המסווג הנוסף:

$$Z_3 = \sum_i D_3 (i) \cdot \exp (-a_3 y_i h_3 (x_i )) \\ D_4 (i) = D_3 \cdot \frac{\exp (-a_3 y_i h_3 (x_i ))}{Z_3} = \{0.5,0.2,0.3\}$$

לבסוף המסווג עם שגיאה אפס המתקבל היינו:

$$H(x) = sign(\sum_{t=1}^3 (\alpha_t h_t (x)))= \{-1,+1,-1\}$$

AdaBoost חלק מעשי

האתגר: בחזרה לטיטניק

ננסה לחזות האם נוסע בטיטניק ישרוד או לא על סמך רישום ונתונים של הנוסעים.

Dataset: The Titanic Manifest

ניתן להוריד את הdataset מהקישור הזה

🕵️ Data Inspection

התרשמות ראשונית ממאגר המידע, עשר שורות ראשונות מהרשומות:

סה”כ ישנם $N=1001$ רשומות במאגר מידע.

The Data Fields and Types

נעשה שימוש בשדות (מאפיינים) הבאים:

• pclass: מחלקת הנוסע: 1, 2 או 3
• sex: מין הנוסע
• age: גיל הנוסע
• sibsp: מס’ של אחים ובני זוג של כל נוסע על האוניה
• parch: מס’ של ילדים או הורים של כל נוסע על האונייה
• fare: המחיר שהנוסע שילם על הכרטיס
• embarked: הנמל בו עלה הנוסע על האונייה (C = Cherbourg; Q = Queenstown; S = Southampton)
• survived: התיוג, האם הנוסע שרד או לא

📉 התרשמות ראשונית בעזרת גרפים

נציג את היחס בין המחלקות (שורדים ונספים) עבור המאפיינים:

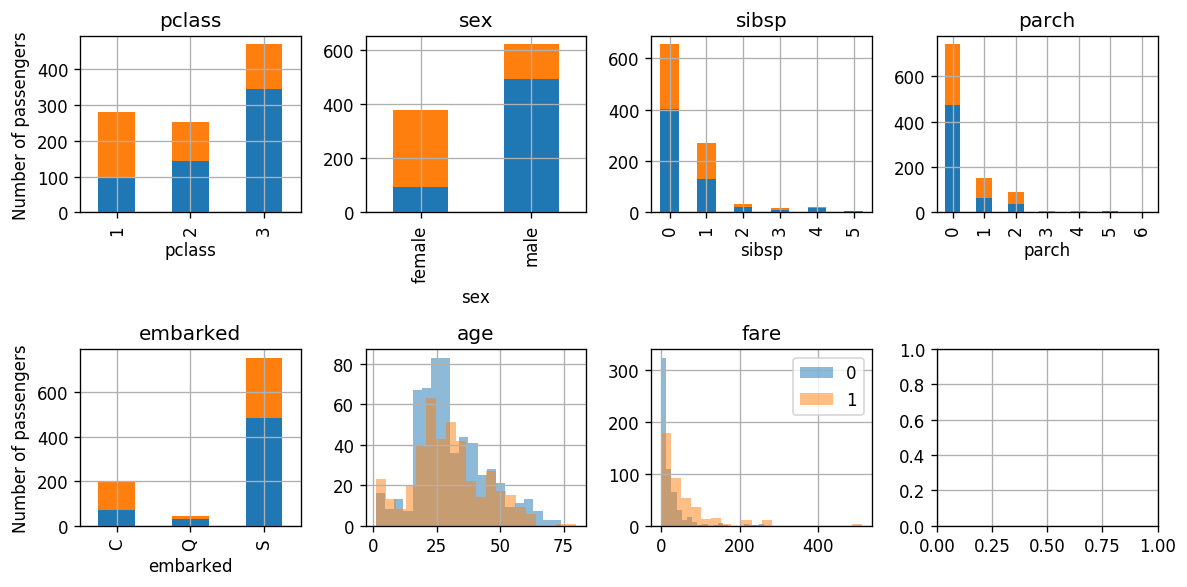
📜 הגדרת הבעיה :#

• משתנים אקראיים:
  • $x_i$ : מאפייני הנוסע
  • $y_i$ : תיוג הנוסע, שרד או נספה

נמצא מסווג $\hat{y}=h^*\left(\boldsymbol{x}\right)$ אשר מביא למינימום את ה- miscalssification rate:

$$h^*=\underset{h}{\arg\min}\ E\left[I\left\lbrace h\left(\boldsymbol{x}\right)\neq y\right\rbrace\right]$$

💡 Model & Learning Method Suggestion: Stumps + AdaBoost

.נשתמש בעץ בינארי בעל עומק אחד (נקרא Stump), שבעצם מסווג על פי מאפיין בודד בשילוב של אלגוריתם AdaBoost

הערה: ניתן להגיד שהשילוב הנ”ל הוא וריאציה של Random Forest, אלגוריתם שמשלב מספר עצים. כמו כן הטכניקה הזאת נקראת גם Ensemble.

עבור קריטריון בניית עץ נשתמש בGini אינדקס ממושקל הנובע מה-data הממושקל. עבור חלוקה של ה-data לשני סטים $\mathcal{C}_1$ and $\mathcal{C}_2$ , וסט המשקולות של הדגימות $\left\lbrace w_i\right\rbrace$ נקבל את Gini אינדקס ממושקל:

$$N_1=\sum_{i\in\mathcal{C}_1}w_i\\ N_2=\sum_{i\in\mathcal{C}_2}w_i\\ p_1=\frac{1}{N_1}\sum_{i\in\mathcal{C}_1}w_iI\left\lbrace y_i=1\right\rbrace\\ p_2=\frac{1}{N_2}\sum_{i\in\mathcal{C}_2}w_iI\left\lbrace y_i=1\right\rbrace\\ G=N_1p_1\left(1-p_1\right)+N_2p_2\left(1-p_2\right)$$

פרמטרים נלמדים:

• החלוקה המתבצעת על ידי כל עץ.
• משקול כל עץ: $\alpha_i$.

Hyper-parameters

ההיפר פרמטרי היחידי הינו קריטריון העצירה עבור אלגוריתם Adaboost שעבורו מוחלט מס’ עצי ההחלטה שמשולבים במסווג הסופי.

📚 חלוקת ה-dataset

נחלק ל 80% סט אימון ו 20% סט בוחן.

⚙️ אימון

נאתחל את המודל ונציג את עשר השורות הראשונות של הdataset הממושקל וההתפלגות לפי המאפיינים:

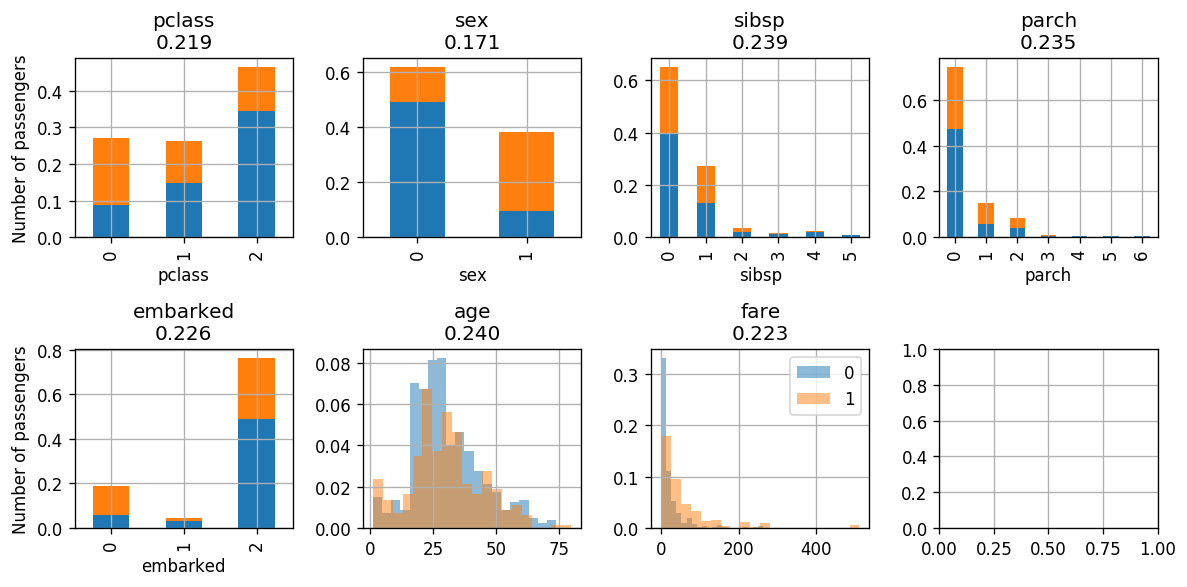
אינדקס Gini המושקלל מצויין בכותרת של כל גרף. בכל איטרציה של Adaboost נבחר את העץ שיפעל על המאפיין בעל האינדקס הנמוך ביותר. כאשר במקרה זה נבחר לפי מין הנוסע.

Iteration: $t=1$

לאחר איטרציה בודדת של סיווג לפי מין קיבלנו:

• שגיאה: 0.22
• $\alpha$: 0.6320312618746508
• Classifing sex according to: {0: [0], 1: [1]}

נציג את המשוקל של ה-data מחדש, וההתפלגויות החדשות:

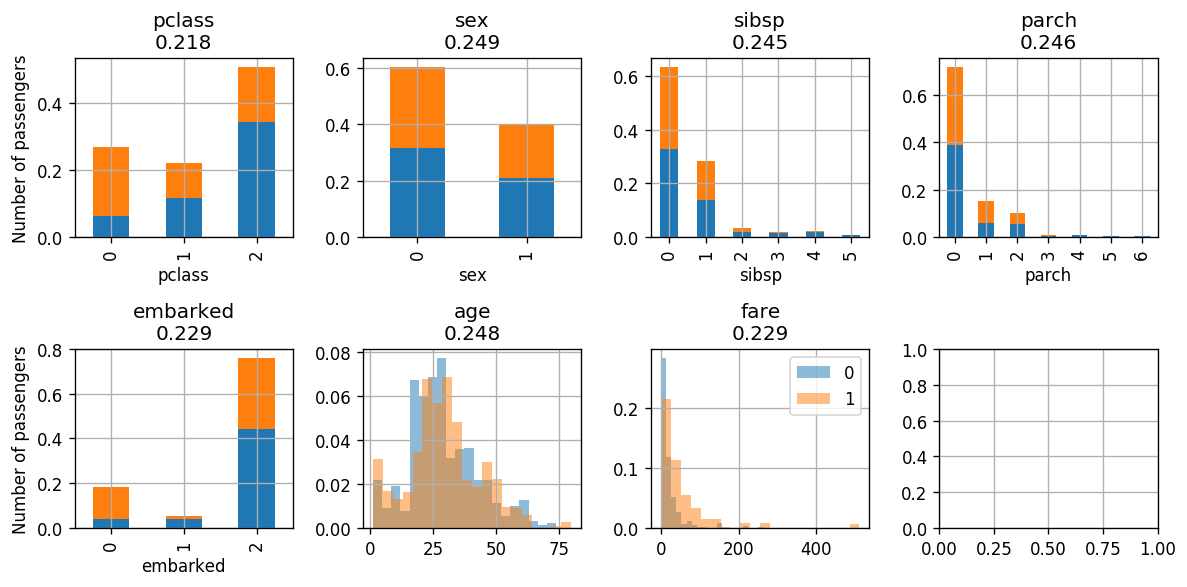
נבחין בכך, שככל שנתקדם באיטרציות של האלגוריתם, ה-data הממושקל יתפלג באופן אחיד כפונקציה של המחלקות, כלומר ההתפלגות של הדגימות שעבורן $y=1$ זהה להתפלגות של הדגימות שעבורן $y=-1$.

כתוצאה מכך, הסיווג על פי מאפיין בודד יהיה קשה יותר והשגיאה למסווג בודד תתקרב ל-0.5, ובאופן ישיר המשקל של כל מסווג $\alpha_t$ ידעך.

בשלב הבא נסווג לפי pclass:

Iteration $t=2$

לאחר איטרציה נוספת של סיווג לפי מחלקת נוסע קיבלנו:

• שגיאה: 0.66
• $\alpha$: -0.34
• Classifing pclass according to: {1: [0], 0: [1, 2]}

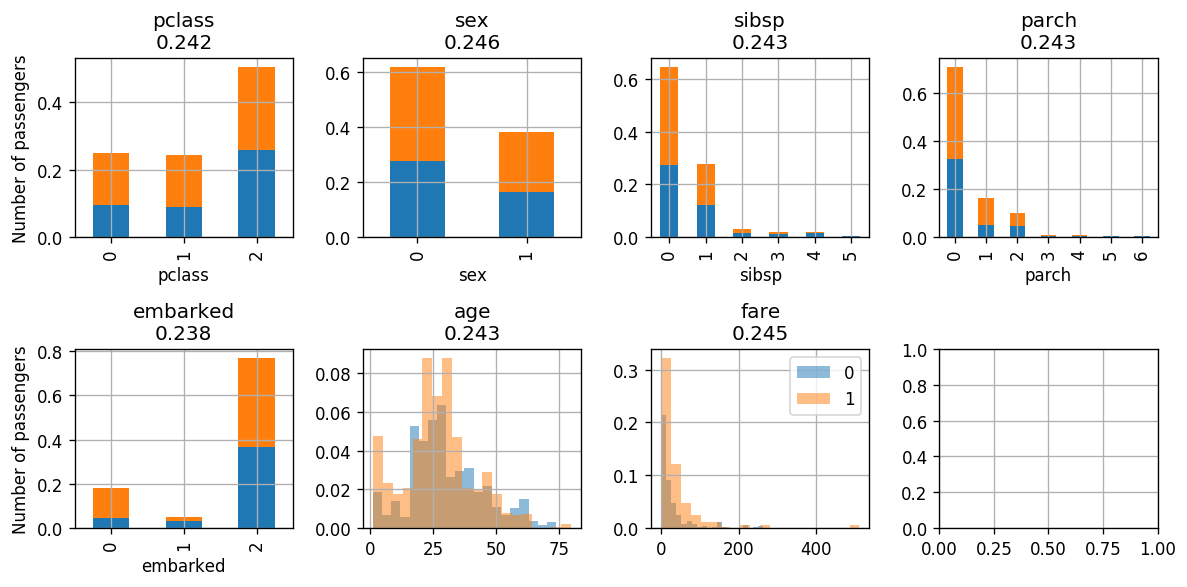
באיטרציה השלישית נסווג לפי embarked:

Iteration $t=3$

• שגיאה: 0.53
• $\alpha$: -0.06
• Classifing embarked according to: {1: [0], 0: [1, 2]}

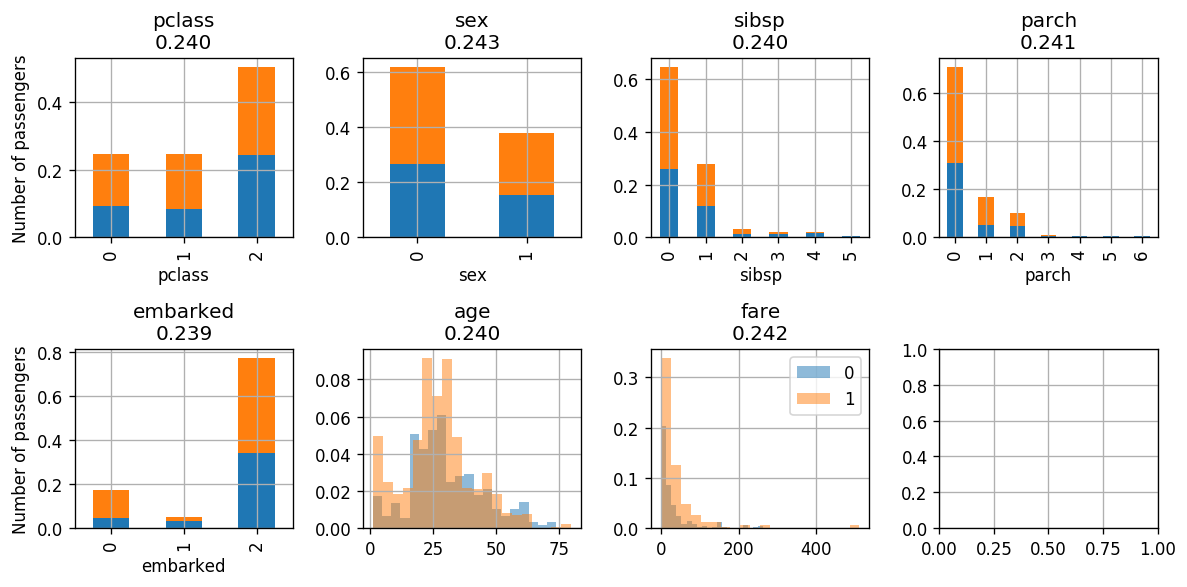
נשים לב שגם אחרי האאינטרציה השלישית קיבלנו את האינדקס הנמוך ביותר עבור embarked. על כן באיטרציה הבאה נסווג עלפיו (ואפשר כבר לנחש שלא נשתפר בביצועים)

Iteration $t=4$

• שגיאה : 0.5000000000000001
• $\alpha$: -2.2204460492503136e-16
• Classifing embarked according to: {1: [0], 0: [1, 2]}

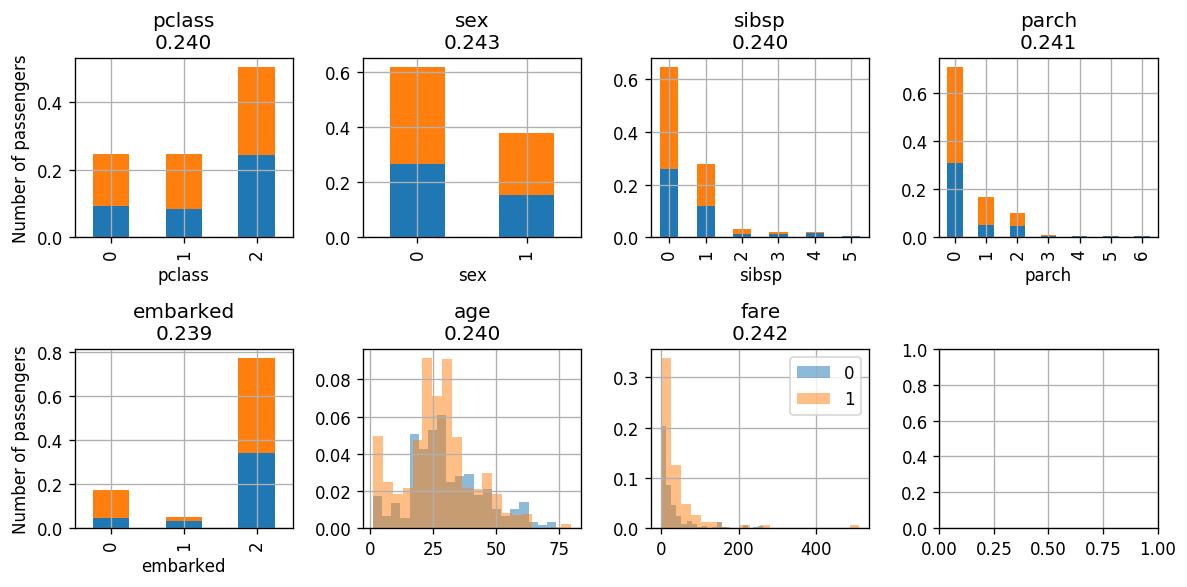
באיטרציה האחרונה קיבלנו ששגיאת המסווג קרובה ל 0.5 והמשקל שלו $\alpha_t \approx 0$, לכן ניתן להפסיק את תהליך הלימוד.

⏱️ ביצועים:

נריץ את האלגוריתם המאומן על סט המבחן ונקבל שהסיכון היינו: $0.225$