046195
  • «previous
  • next»
  • Open Slides

תרגול 10

CNN

תיאוריה

Convolutional Neural Networks (CNN) - רשתות קונבולוציה

אחת התכונות של מודל MLP (Fully Connected (FC) network) הינה חוסר רגישות לסדר בכניסות לרשת. תכונה זו נובעת מכך שכל היחידות בכל שכבה מחוברות לכל היחידות בשכבה העוקבת. במקרים רבים תכונה הינה תכונה רצויה, אך היא באה במחיר של מספר רב של פרמטרים. במקרים בהם למידע אשר מוזן לרשת יש מבנה או תלות מרחבית, כלומר יש משמעות לסדר של הכניסות, נרצה לנצל את ההיתרון המרחבי של הכניסות בעת תכנון ארכיטקטורת הרשת. דוגמא לסוג כזה של מידע הן תמונות. רשתות קונבולציה הינם סוג אחד רשתות feed-forward בעלת ארכיטקטורה אשר מנצלת את התלות המרחבית בכניסות לכל שכבה.

1D Convolutional Layer

שכבת קונבולוציה חד-ממדית הינה שכבה ברשת אשר מבצעת פעולת קרוס קורלציה בין וקטור הכניסה של אותה שכבה ווקטור משקולות באורך :

וקטור המשקולות של שכבת הקונבולציה נקרא גרעין הקונבולוציה (convolution kernel)

הערה: בניגוד לשמה, שכבת קונבולוציה מחשבת קרוס-קורלציה, ולא קונבולוציה, אשר המוגדרת על ידי: .

ובאופן גרפי:

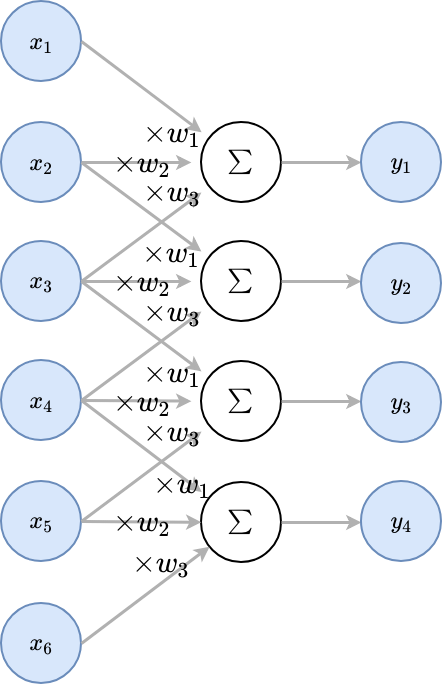
Conv layer

נשים לב להבדלים מרשת FC:

  1. היציאות מחוברות רק לחלק מהכניסות, כאשר הכניסות קרובות אחת לשניה
  2. כל היציאות מופקות מאותן משקולות

ההנחות שמובילות לארכיטקטורה זאת:

  • הקשר בין כניסות קרובות הוא יותר חזק ומשמעותי מאשר כניסות רחוקות.
  • אזורים שונים במידע הנכנס לרשת מתנהגים במידה מסויימת באופן זהה.

שכבת קונבולוציה מורידה באופן דרסטי את מס’ המשקולות לעומת שכבת FC. בשכבת FC קיימות משקולות בעוד שלשכבת קונבולציה יש משקולות.

דרך נוספת להצגת שכבת קונבולוציה:

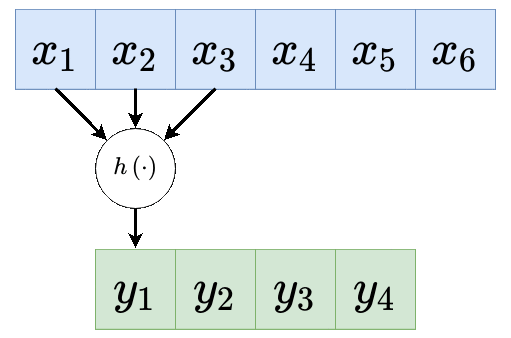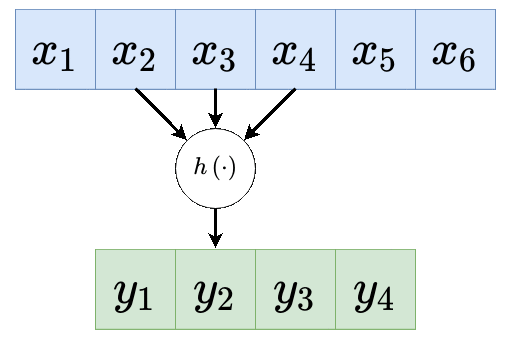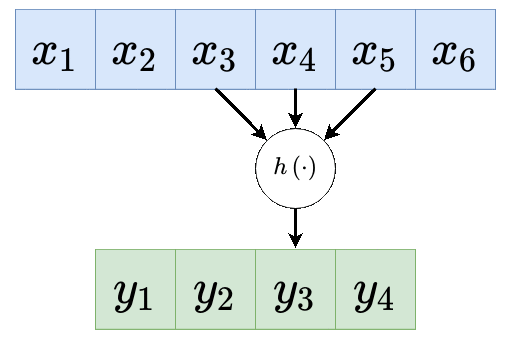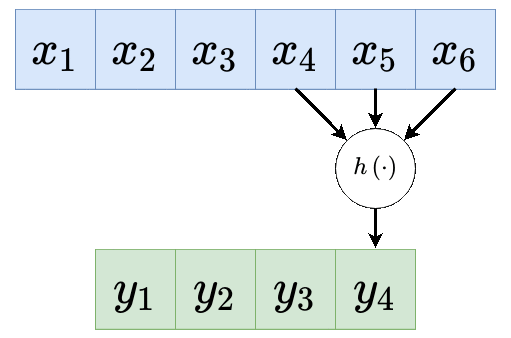
Conv layer

כאשר: , ו- היינו איבר ההסט.

אקטיבציה לא לינארית

בדומה לשכבות FC, בשכבת קונבולציה נעשה שימוש בפונקציות אקטיבציה לא לינאריות לאחר פעולת הקונבולציה שהיינה פעולה לינארית. גם כאן השימוש הכי נפוץ היינו בפונקציית ReLU: , אך ניתן להשתמש בכל פונקציה אחרת. בפועל מפרידים בין שכבת הקונבולוציה לבין פעולת האקטיבציה והארכיטקטורה נראת כך:

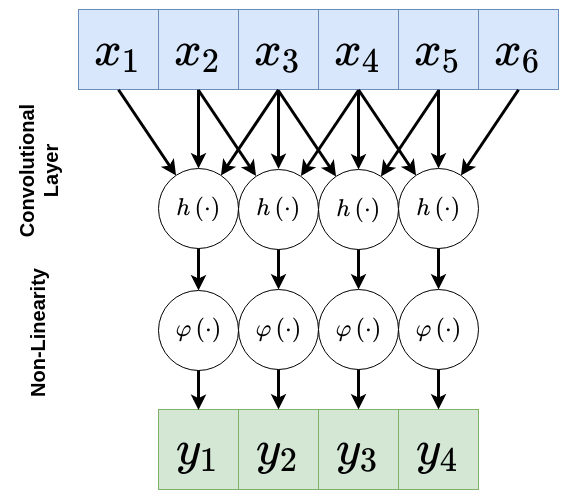
Conv layer + non-linear layer

קלט רב-ערוצי

במקרים רבים נרצה ששכבת הקונבולציה תקבל קלט רב ממדי, לדוגמא, תמונה בעלת שלושה ערוצי צבע או קלט שמע ממספר ערוצי הקלטה. מבנה זה מאפשר לאזור מרחבי בקלט להכיל אינפורמציה ממספר ערוצי כניסה.

במקרים אלו הניורון יהיה פונקציה של כל ערוצי הקלט:

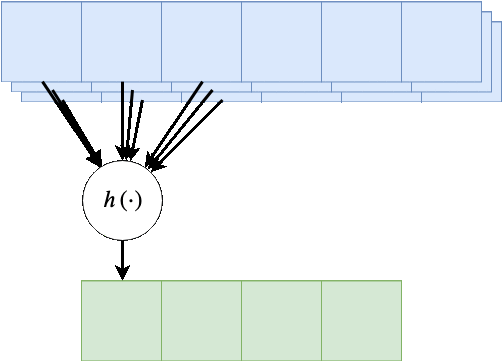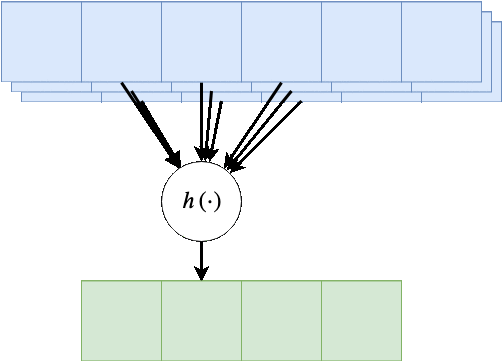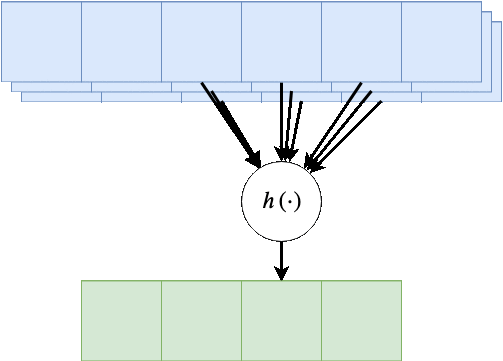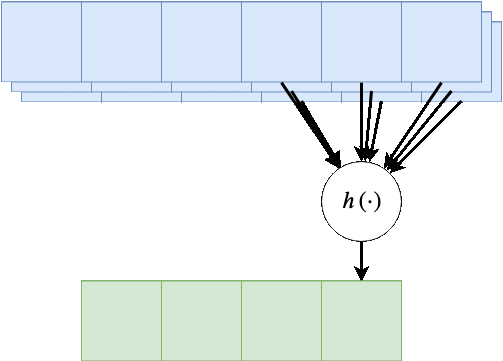
multi-channel conv layer

הפונקציה היינה קומבינציה לינארית של כל ערוצי הקלט, לרוב מסיפים איבר הסט ופונקציית אקטיבציה.

פלט רב-ערוצי

בנוסף, נרצה לרוב להשתמש ביותר מגרעין קונבולוציה אחד, במקרים אלו נייצר מספר ערוצים ביציאה בעבור כל אחד מגרעיני הקונבולוציה.

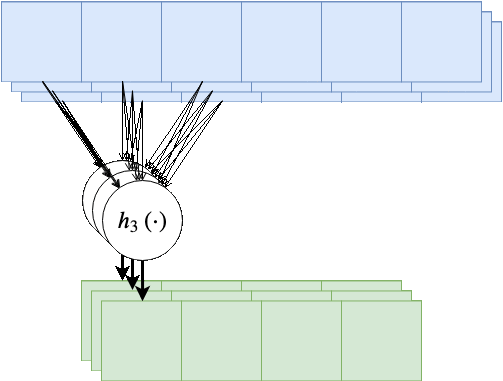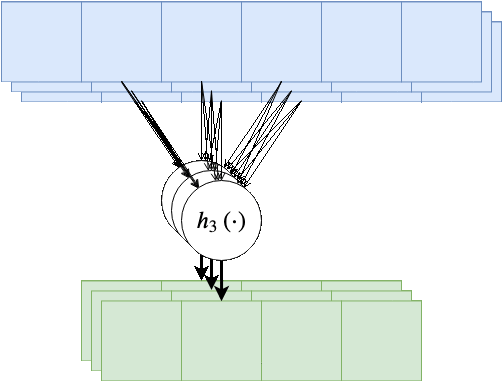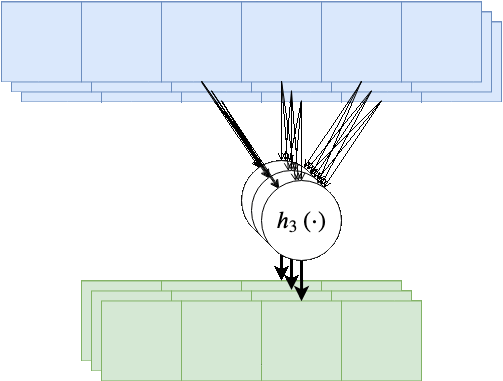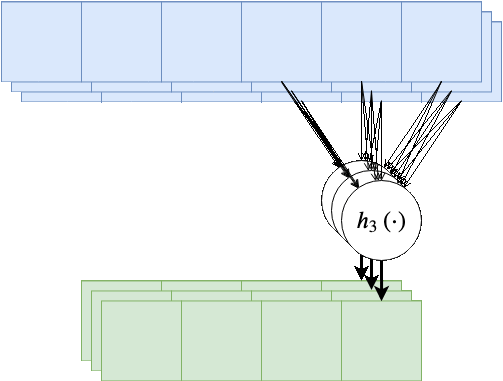
multi-input multi-output conv layer

בשכבות אלו אין שיתוף של משקולות בין ערוצי הפלט השונים, כלומר כל גרעין קונבולציה הוא בעל סט משקולות יחודי הפועל על כל הערוצי הכניסה על מנת להוציא פלט יחיד. מספר הפרמטרים בשכבת כזאת היינו:

כאשר:

  • - מספר ערוצי קלט.
  • - מספר ערוצי פלט.
  • - גודל הגרעין.

היפר-פרמטרים של שכבות קונבולוציה

בנוסף לפרמטרים של גודל הגרעין ו מספר ערוצי הפלט, שהינם היפר-פרמטרים של שכבת הקונבולוציה, מקובל להגדיר גם את הפרמטרים הבאים:

Padding - ריפוד

משום שפעולת קונבולציה היינה מרחבית, בקצוות הקלט ישנה בעיה שאין ערכים חוקיים שניתן לבצע עליהם פעולות, לכן נהוג לרפד את שולי הקלט (באפסים או שכפול של אותו ערך בקצה)

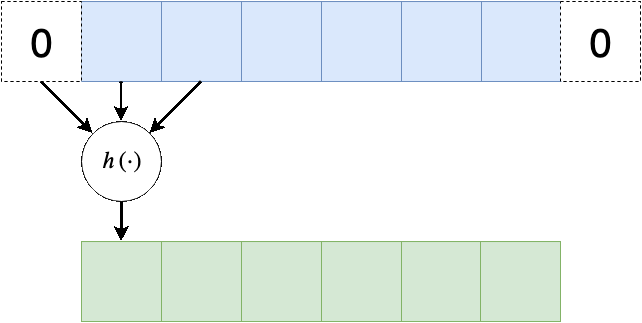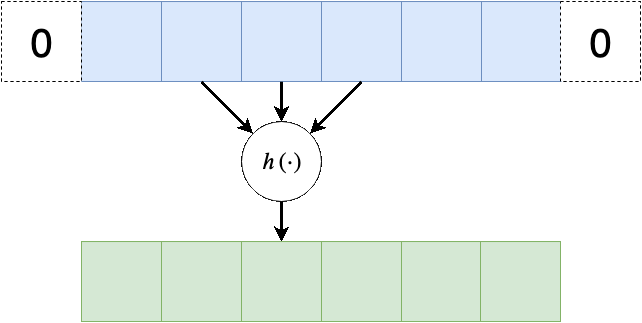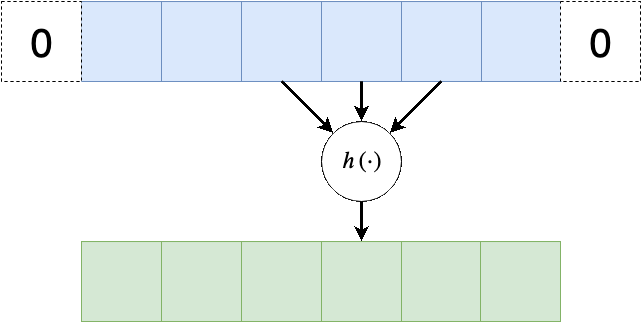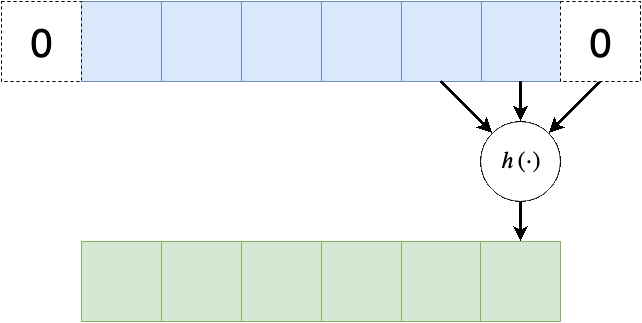
padding

Stride - גודל צעד

ניתן להניח שלרוב הקשר המרחבי נשמר באזורים קרובים, לכן על מנת להקטין בחישוביות ניתן לדלג על הפלט ולהפעיל את פעולת הקונבולציה באופן יותר דליל. בפשטות: מדלגית על היציאות בגודל הצעד. לרוב גודל הצעד מסומן ב , בדוגמא הבאה גודל הצעד היינו .

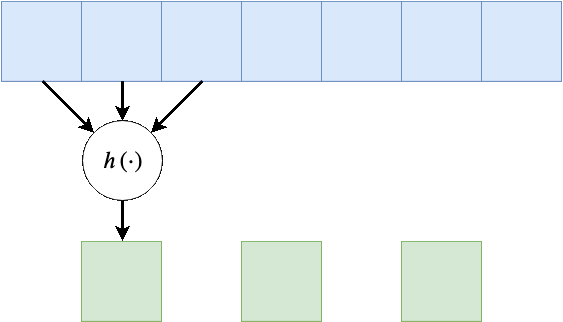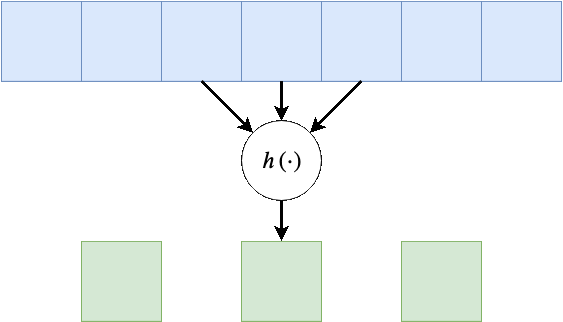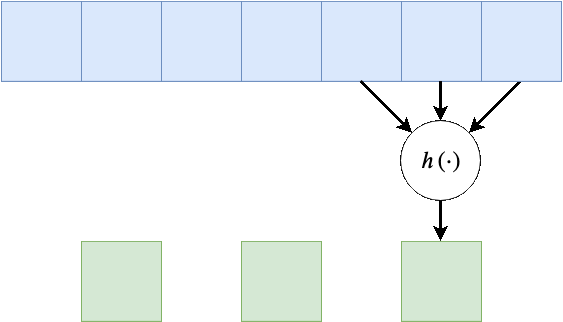
stride

Dilation - התרחבות

שוב על מנת להקטין בחישובית, אפשר לפעול על אזורים יותר גדולים תוך הנחה שערכים קרובים גיאוגרפית הם בעלי ערך זהה, על כן נרחיב את פעולת הקונבולציה תוך השמטה של ערכים קרובים. לרוב נסמן את ההתרחבות ב בדוגמא הבאה .

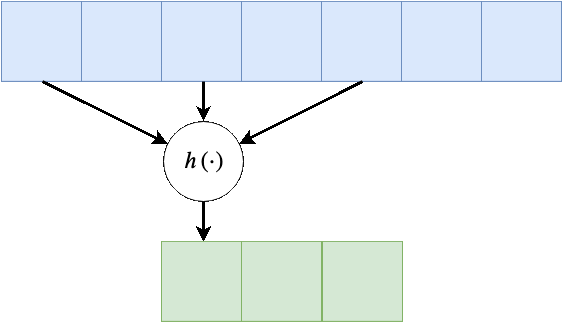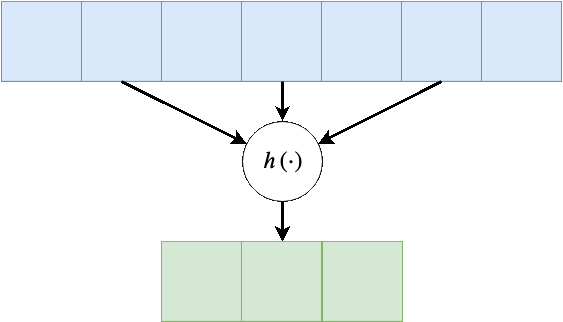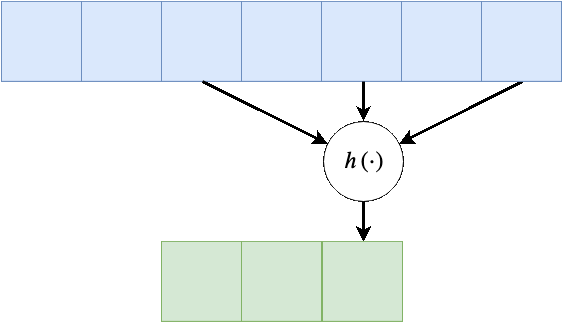
dilation

דגש: צעידות מצמצמות את הפלט, התרחבות גם כן מצמצמת את הפלט אך על חשבון התרחבות על הקלט.

Max Pooling

לרוב ב CNN נעשה שימוש בשכבת נוספות על מנת לצמצם את הגודל המרחבי של הקלט. שכבה כזאת לדוגמא היינה שכבת Max Pooling, שכבה זאת לוקחת את המקסימום מבין ערכי הכניסה. המוטיבציה לפעולה זאת היינה שהערכים הגבוהים מייצגים מאפיינים בעלי יותר אינפורמציה על כן נרצה לשמר את הערכים אלה על חשבון המאפייינים בעלי פחות אינפורציה.

בדוגמא הבאה גודל ב Max Pooling היינו 2 וגודל הצעד (stride) גם כן 2:

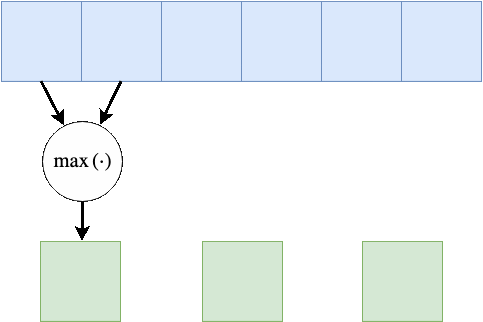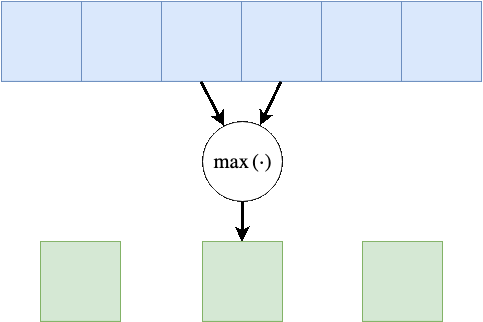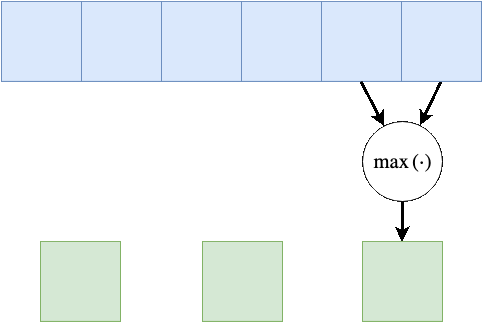
max pooling

בשכבה זאת אין פרמטרים נלמדים, אך גודל הגרעין היינו היפר-פרמטר נוסף.

2D Convolutional Layer

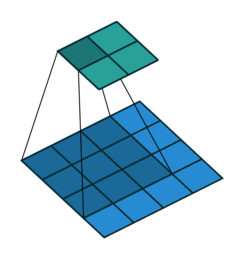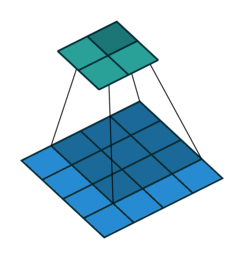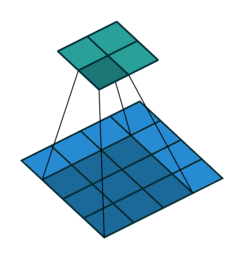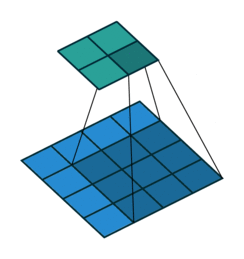
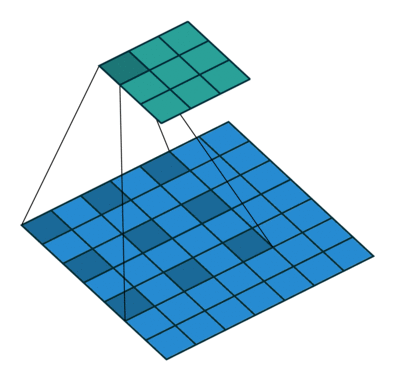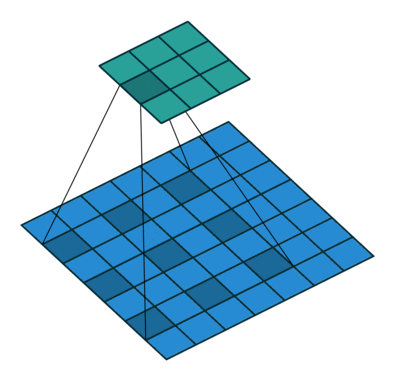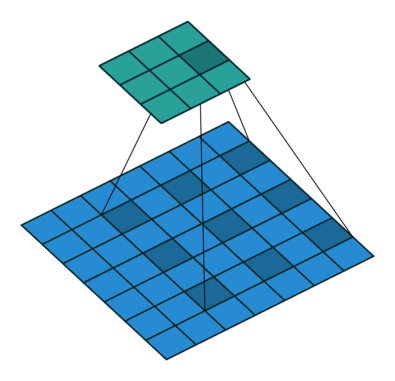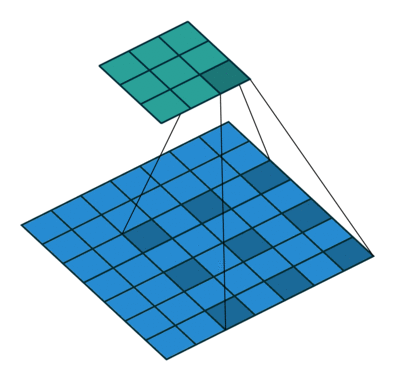
עבור קלט דו-ממדי (תמונות), הקלט מסודר כמטריצה. ופעולת הקונבולוציה (קרוס-קורלציה כפי שאתם מכירים) נראה כך:

כאשר השכבה הכחולה היא הקלט והשכבה הירוקה היא הפלט

kernel size=3
padding=0
stride=1
dilation=1
kernel size=4
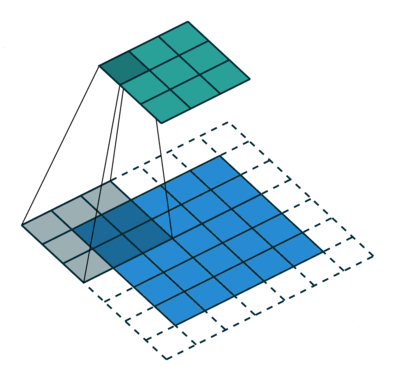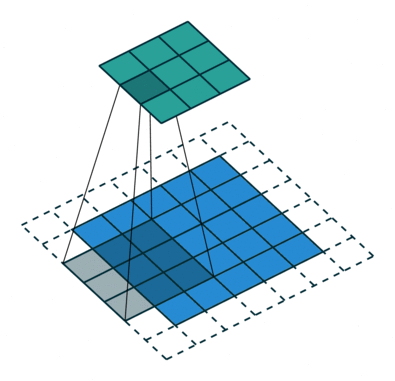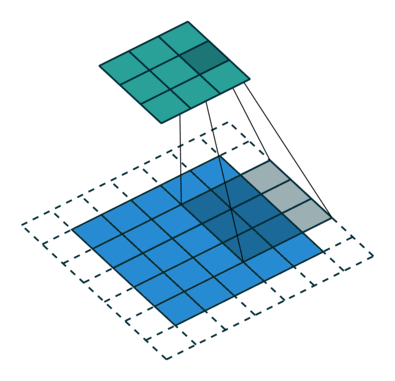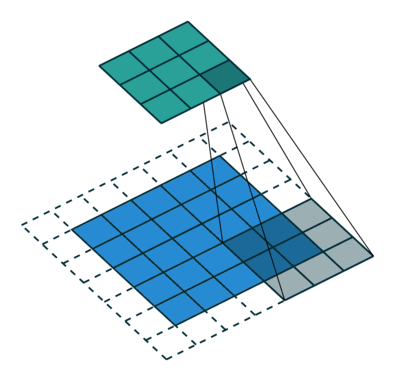
padding=2
stride=1
dilation=1
kernel size=3
padding=1
stride=1
dilation=1
(Half padding)
kernel size=3
padding=2
stride=1
dilation=1
(Full padding)
kernel size=3
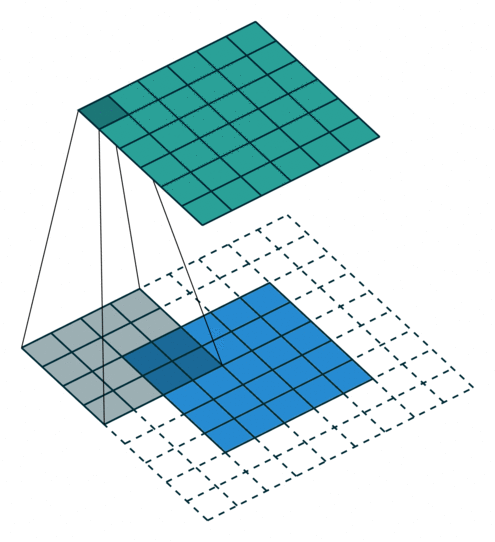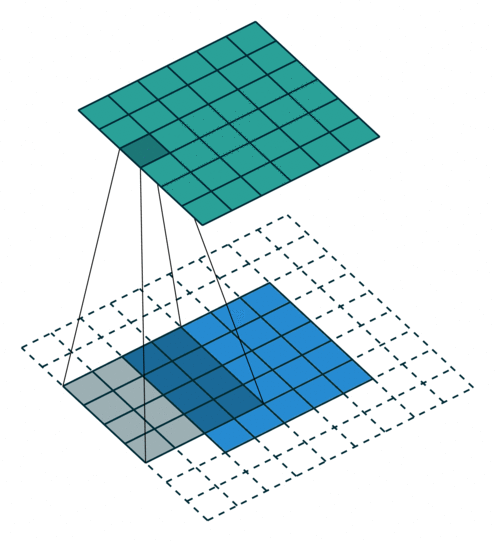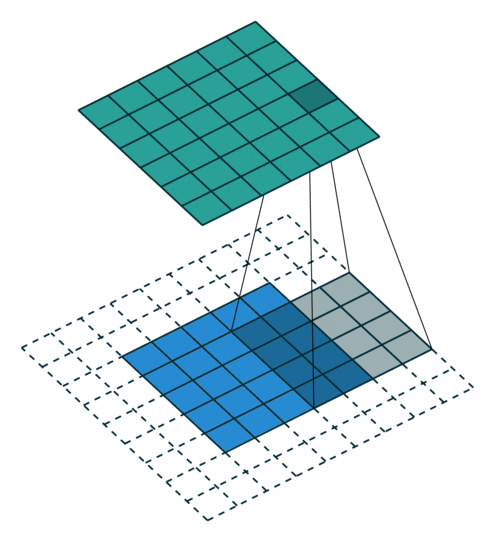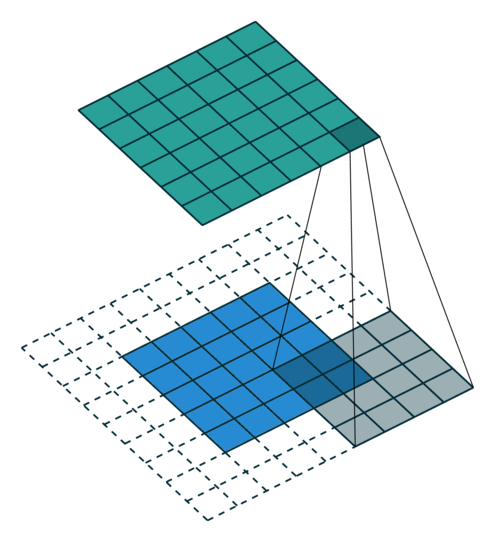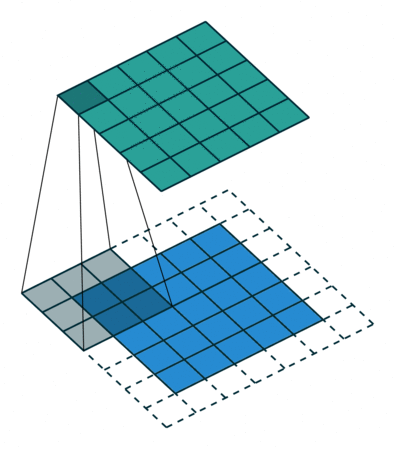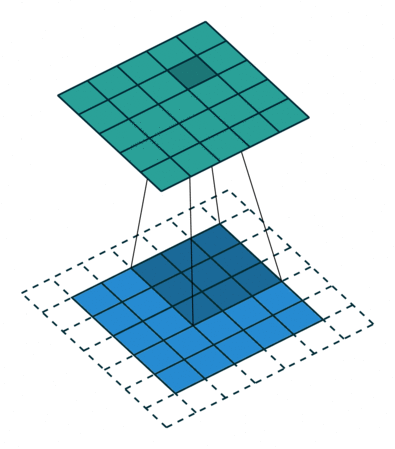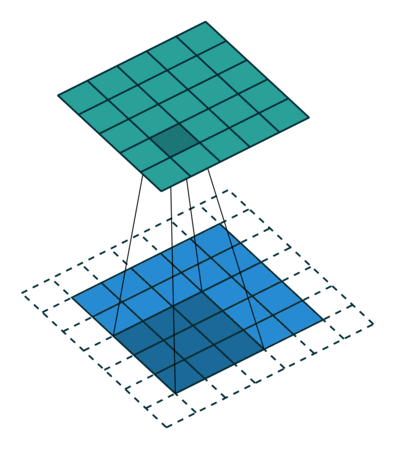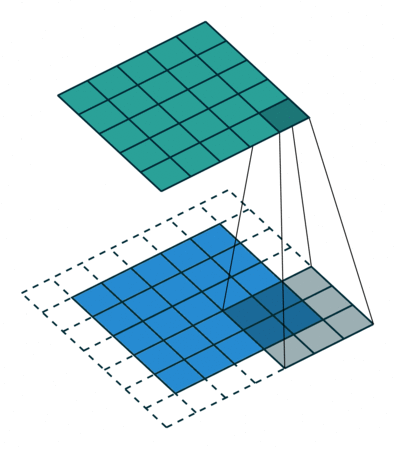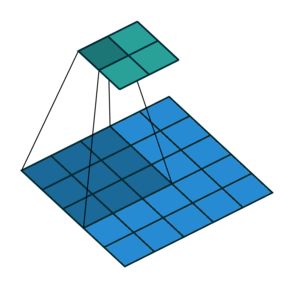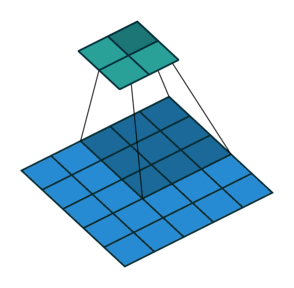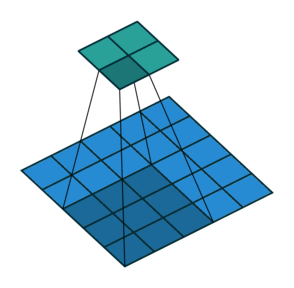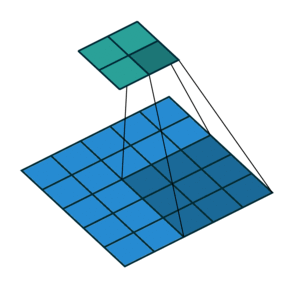
padding=0
stride=2
dilation=1
kernel size=3
padding=1
stride=2
dilation=1
kernel size=3
padding=1
stride=2
dilation=1
kernel size=3
padding=0
stride=1
dilation=2
  • [1] Vincent Dumoulin, Francesco Visin - A guide to convolution arithmetic for deep learning(BibTeX)

תרגילים

תרגיל 10.1

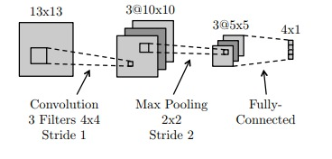
נתונה רשת קונבולוציה קטנה, הממירה תמונה בגודל 13×13 לווקטור מוצא בגודל 4×1. הרשת מורכבת מהפעולות הבאות:

  • שכבת קונבולוציה עם 3 פילטרים (גרעינים) בגודל 4x4
  • פונקציית אקטיבציה Relu
  • max pooling 2x2 עם stride=2
  • שכבת Fully-connected (FC)
  • פונקציית אקטיבציה Relu

ברשת זאת אין שימוש בbias.

network

א) כמה פרמטרים נלמדים יש בשכבת הקונבולוציה

ב) כמה פעולות אקטיבציה מבוצעות (Relu) במעבר קדמי אחד (forward pass)?

ג) כמה משקולות יש בכל הרשת?

ד) האם רשת בקישוריות מלאה (FC) בעלת גודל שכבות זהה – כלומר רשת זהה שבה שכבת הקונבולוציה מוחלפת בשכבת FC, יכולה לייצג את אותה הפונקציה אותה ממשת הרשת המקורית?

ה) מה ההבדל העיקרי בין רשת CNN ל FC שיכולות לייצג את אותו מסווג?

פתרון:

א) סה”כ 48 פרמטרים. קיימים 3 פילטרים בגודל 4×4, לכן 3⋅4⋅4=48.

ב) מבוצעות 304 פעולות Relu. פעולת האקטיבציה מתבצעת לכל מאפיין במוצא שכבת הקונבולוציה ועוד 4 במוצא שכבת הFC. כלומר:

ג) 348 פרמטרים. נפרט את החישוב. בשכבת הקונבולוציה יש 48 פרמטרים (סעיף א), בשכבת הFC יש כניסות שמחוברות ל יציאות, סה”כ .

ד) כן, הרשת עם שכבת הקונבולוציה הינה מקרה פרטי של רשת FC, עם בחירה ספציפית של המשקולות.

ה) הרשת עם שכבת הקונבולוציה מתארת תת-תחום של מרחב הפונקציות שאותה יכולה לתאר רשת הFC. היתרון שברשת עם שכבת הקונבולוציה הינה שהיא עושה זאת על ידי מספר קטן משמעותית של פרמטרים. לכן, בהנחה שניתן לקרב במידה טובה מספיק את פונקצייית המטרה על ידי פונקציות מתת-תחום זה, היא תניב תיטה פחות לoverfit ולכן בעלת סיכוי להניב תוצאות טובות יותר. לשם השוואה ברשת הFC ישנם כ50k פרמטרים.

תרגיל 10.2

התמך או הrecptive field של משתנה מסויים ברשת מוגדר להיות כל התחום בכניסה אשר משפיע על אותו המשתנה.

א) מצאו את הrecptive field של ערך מסויים במוצא של שלוש שכבות קונבולוציה רצופות עם גרעין של .

ב) רשמו באופן מטריצי את פעולת הקונבולוציה.

פתרון

א) הrecptive field של שלוש שכבות קונבולוציה רצופות בגודל הינו איזור בגודל . נדגים זאת:

קונבולוציה ראשונה:

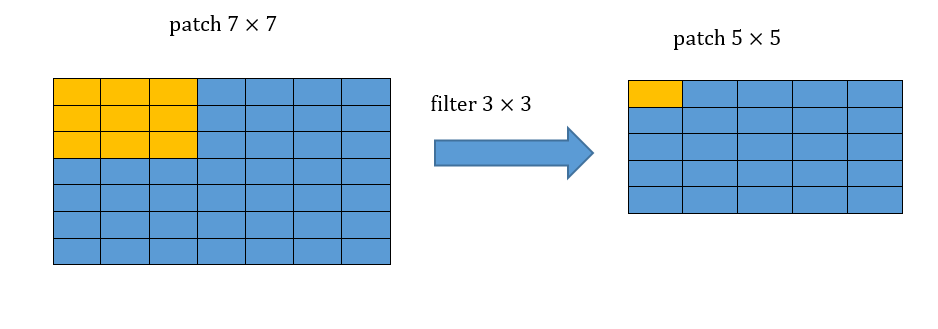
First convilution

קונבולוציה שניה:

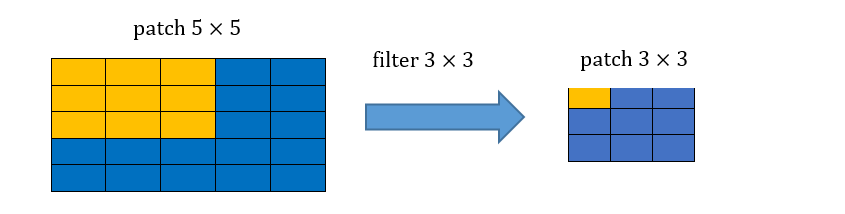
Second convilution

קונבולוציה שלושית:

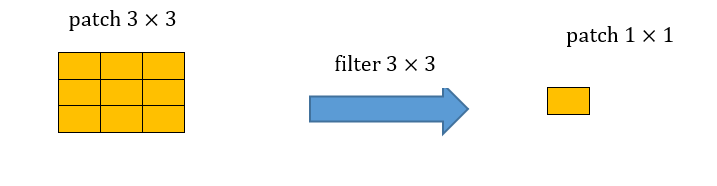
Third convilution

ב. נרשום את הפילטרים ככפל מטריצות, עבור הפילטר הראשון:

ובאופן זהה עבור פילטר מס’ שתיים ושלוש.

נרשום את הקלט בצורה וקטורית:

וסה”כ נקבל:

סכמות אתחול

מוטיבציה

ראינו בתרגול 8 דוגמה שהמחישה כי בחירה לא טובה של האתחול יכולה להוביל לכך שפונקציית האקטיבציה תהיה באזור של רוויה ולכן העדכון של המשקולות באלגוריתם GD יהיה מאוד איטי ולא אפקטיבי

  • אם המשקולות של הרשת מתחילות בערכים קטנים מדי אז האות דועך ככל שהוא מתקדם לאורך הרשת ולא מחלחל בצורה טובה לשכבות המתקדמות. (vanishing gradients).
  • אם המשקולות של הרשת מתחילות בערכים גדולים מדי אז האות גדל בין שכבה לשכבה מה שיכול לגרום לבעיות באימון (חריגה מתחום ייצוג, exploding gradients).

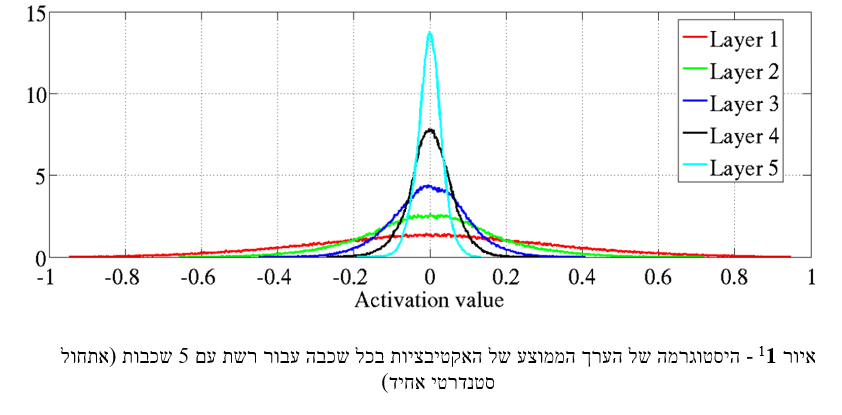
initilization 1

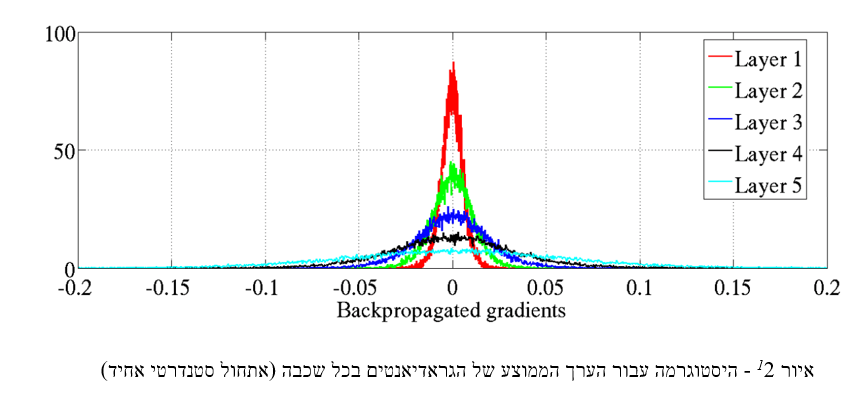
initilization 2

  • ניתן לראות באיורים כי האות לא מפעפע בצורה טובה דרך הרשת:
    • באיור הראשון אנו רואים כי ככל שמתקדמים לעומק הרשת האקטיבציות דועכות, כלומר, יש יותר אקטיבציות עם ערכים מאוד קרובים לאפס.
    • באיור השני אנו רואים את הבעיה של vanishing gradients שלמדנו בתרגול הקודם.

המטרה:

נרצה למצוא אתחול טוב של המשקולות אשר יאפשר לאות לפעפע דרך הרשת בצורה טובה.

תרגיל 10.3

בשאלה זו נרצה למצוא סכמת אתחול עבור משקולות הרשת. לשם כך, נתחיל מלבחון נוירון ליניארי בודד.

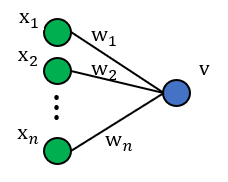
Graph

הערה: אם הממוצע של המוצא הוא 0 והשונות נשארת קבועה בין שכבות (לא דועכת או מתפוצצת) – אין התפוצצות או העלמות של האות לאורך הרשת. לכן, בסעיפים הבאים נתעניין בחישוב הממוצע והשונות של המוצא . ספציפית, נרצה להראות כי ואז לחשב את השונות של המוצא על מנת לראות מה עלינו לדרוש על אתחול המשקולות על מנת להבטיח כי שונות המוצא תישאר קבועה לאורך הרשת.

א) נניח כי כל רכיבי המשקולות וכל רכיבי הכניסה הם משתנים אקראיים IID. בנוסף, נניח כי התפלגות המשקולות סימטרית סביב 0.

  1. חשבו את התוחלת של המוצא כתלות בתוחלות של המשקולות והכניסה. בפרט, הראו כי .

  2. הראו כי לכל זוג משתנים אקראיים בלתי תלויים מתקיים:

  3. כעת, נניח כי לכל : (בסעיף הבא נראה הצדקה להנחה זו). השתמשו בנוסחה מהסעיף הקודם על מנת לבטא את השונות של באמצעות השונות של .
  4. כיצד ניתן לשמור על השונות של המוצא זהה לשונות של כל אחת מרכיבי הכניסה ?

ב) כעת, נרצה להרחיב את הסכמה לנוירונים לא ליניאריים:

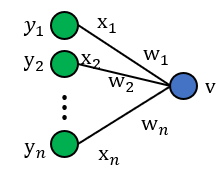
Graph

כלומר, כעת מתקיים כי כאשר היא פונקציית האקטיבציה ו-

אנו נניח כי ניורון זה הוא חלק מרשת עמוקה, כלומר, נניח כי הם המוצאים של ניורונים מהשכבה הקודמת ברשת.

הערה: בסעיף הבא נראה כי התוחלת של המוצא איננה 0 עבור אחת מהאקטיבציות שלמדנו בקורס. עם זאת, נראה כי הממוצע לפני האקטיבציה, כלומר, הממוצע של , הוא עדיין 0 לכל . לכן, אין לנו בעיה של התפוצצות הממוצע אם השונות נשארת קבועה בין שכבות (לא דועכת או מתפוצצת) – אין התפוצצות או העלמות של האות לאורך הרשת.

  1. לאילו מפונקציות האקטיבציה הבאות: sigmoid, tahn ו-ReLU, ההנחה שביצענו בסעיף הקודם היא עדיין הנחה “סבירה”? תזכורת:

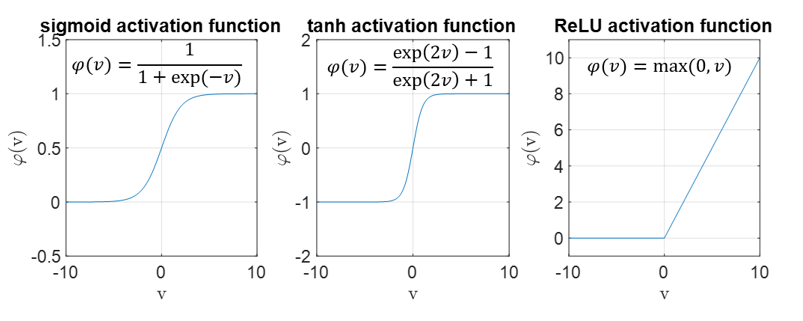
    Activation function

  2. כעת לא נניח דבר על התוחלת של . כיצד ישתנה הביטוי של השונות של מסעיף א.3?
  3. עבור פונקציית האקטיבציה ReLU, בטאו את השונות של באמצעות השונות של אחת הכניסות . הניחו כי

הדרכה: היעזרו בתוצאות הסעיפים הקודמים.

פתרון:

א)

  2. נעזר בקשר :

  3. תחת ההנחה כי התוחלות של המשקולות ושל הכניסה הן 0, הנוסחה שהוכחנו בסעיף הקודם מצטמצמת ל. בנוסף, עבור מוצא הניורון ניתן לכתוב:

    מכיוון שהנחנו שכל המשתנים מפולגים IID נקבל:

  4. קיבלנו בסעיף הקודם כי שונות המוצא הוא שונות הכניסה מוכפל בפקטור של כאשר הוא מספר הניורונים המוזנים לניורון. לכן, על מנת לשמור על שונות זהה בין כניסה למוצא נבחר את אתחול המשקולות כך שיתקיים:

ב)

  1. אם התפלגות המשקולות סימטרית סביב 0, נקבל כי התפלגות סימטרית סביב 0 לכל . לכן, ההנחה עדיין סבירה עבור tanh אך לא עבור ReLU וsigmoid. עבור tanh נקבל:

    כאשר סימנו .

  2. משימוש בתוצאות הסעיפים הקודמים, נקבל:

  3. אם התפלגות המשקולות סימטרית סביב 0, נקבל כי התפלגות סימטרית סביב 0 לכל . לכן, עבור פונקציית אקטיבציה ReLU נקבל:

    נשלב את התוצאה יחד עם תוצאות הסעיפים הקודמים ונקבל:

    לכן, על מנת לשמור על שונות זהה בין כניסה למוצא נבחר את אתחול המשקולות כך שיתקיים:

חלק מעשי

LeNet-5

בחלק זה נעבור על היישום המעשי הראשון של רשתות קונבולוציה. הארכיטקטורה זאת שימשה ב1998 ושימש לזהות ספרות בכתב יד על צק’ים במערכות בנקאיות.

LeNet results

הרשת מקבלת תמונה רמת אפור בגודל 32x32 ומשתמש באריטקטורה הבאה על מנת להוציא וקטור פלט באורך 10 אשר מציג את הסבירות שהתמונה שייכת לכל אחת מ 10 הספרות.

אריכטקטורה

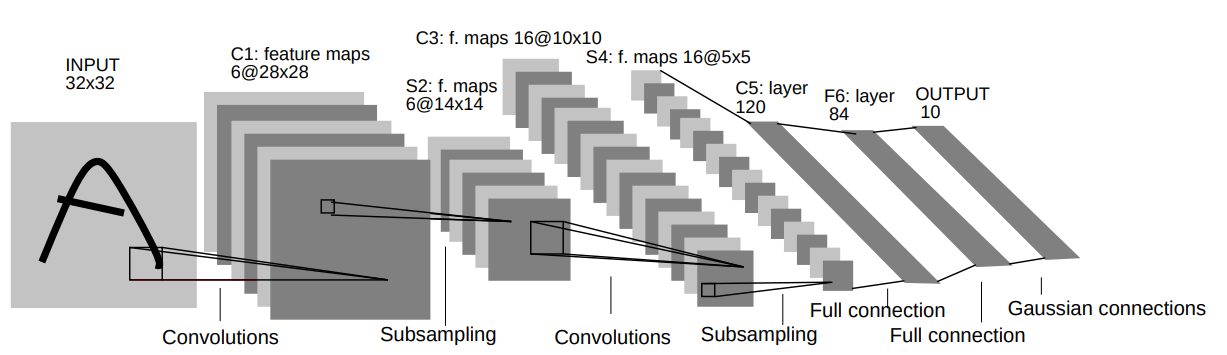
LeNet architecture

ארכיטקטורה זו לא עושה שימוש בריפוד ו-dilation, ואלא אם רשום אחרת stride=1.

  • C1: Convolutional layer + ReLU activation: kernel size=5x5, output channels=6.
  • S2: Max pooling layer: size=2x2, stride=2
  • C3: Convolutional layer + ReLU activation: kernel size=5x5, output channels=16.
  • S4: Max pooling layer: size=2x2, stride=2
  • C5: Convolutional layer + ReLU activation: kernel size=5x5, output channels=120. (this is, in fact, a fully connected layer)
  • F6: Fully connected layer + ReLU: output vector length= 84
  • Output layer: Fully connected layer: output vector length=10

על מנת לייצג את הסתברות שהתמונה שייכת לאחת מהמחלקות נעשה ביציאה שימוש בשכבת Softmax.

Dataset: MNIST

לאימון הרשת נעשה שימוש במאגר המידע MNIST. הוא סט פופולרי מאוד שנעשה בו שימוש נרחב עד היום. הסט מורכב 70000 תמונות בינאריות בגודל 28x28 של ספרות בכתב יד, מתוכן 10000 הינם בסט המבחן.

ניתן להוריד את הסט מ Yann LeCun’s web site או לחילופין, ישרות מ -PyTorch torchvision.datasets.MNIST

mnist

הגדרת הבעיה

  • המשתנים בבעיה:
    • תמונה בגודל 28x28 של סיפרה בכתב יד -
    • ערך הסיפרה: [0-9] -


  • רשת הנוירוניים תשמש כמשפחה הפרמטרית אשר בעזרתה ננסה ללמוד את הפילוג :

  • הלימוד יעשה בעזרת MLE (אשר שקול למזעור של הcross entropy).


  • החזאי אשר ימזער את ה missclassification rate יהיה:

חלוקה של מאגר המידע

משום שהמאגר המידע מחולק כבר לסט מבחן, כל מה שנותר לנו הוא לחלק את סט האימון לסט ולידציה וסט אימון. אין צורך לקחת סט ולידציה גדול משום שהרצת המודל על סט גדול דורשת הרבה משאבים, נקח סט קטן בגודל 1024 על מנת להעריך את ביצועי המודל בתהליך הלמידה באופן מהיר וחסכוני.

לימוד

נשתמש באלגוריתם הגרדיאנט בגרסת ה-mini-batch, או בשמו stochastic gradient descent (SGD), המשמעות הסטוכנסטית הינה שהBatch מוגרל באופן אחיד מתך מאגר המידע. האלגוריתם ישמש למציאת משקולות הרשת להקטנת פונקצית המחיר.

תזכורות: משקולות הרשת הינם המשקולות בגרעיני קונבולוציה, בשכבות FC ואיברי ההסט.

Hyper-parameters

  • הארכיטקטורה של הרשת, שבה לא נעשה כל שינוי.
  • אלגוריתם SDG:
    • גודל צעד הלימוד.
    • גודל הBatch, אשר אותו נשאיר קבוע בגודל 64.
    • מס’ מקסימלי של epochs. epochs - מס המעברים על כל סט האימון

בחירת גודל צעד הלימוד

נבחן את השפעת גדלי צעד לימוד על תהליך הלימוד. נריץ את האלגוריתם למשך epoch אחד עם הגדלים הבאים:

png

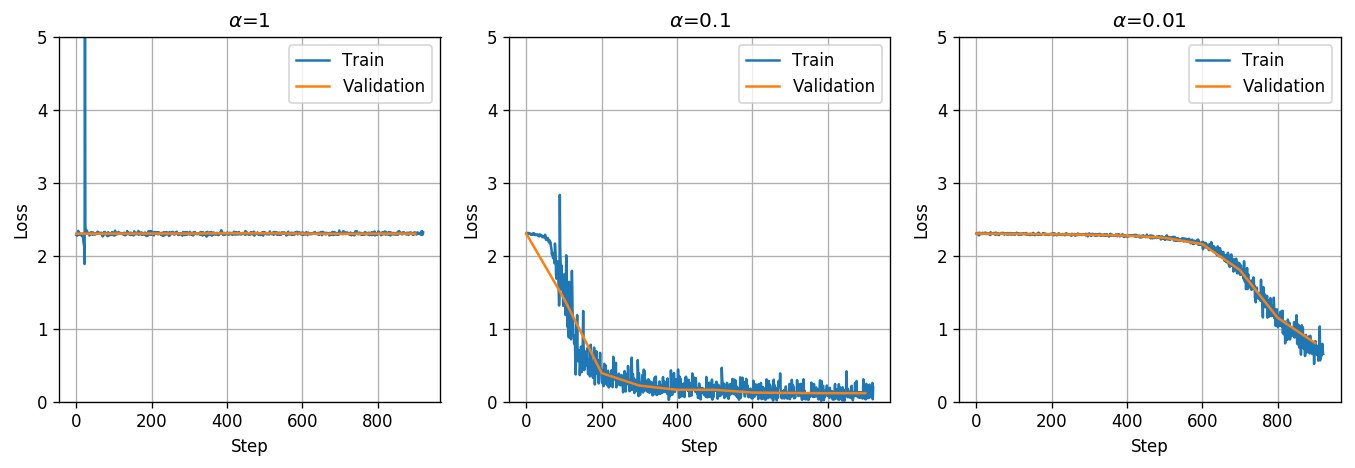
קיבלנו שעבור המערכת לא מצליחה לבצע למידה (להקטין את פונקציית המחיר). ניתן להגיד שצעד הלימוד גדול מידי משום שעבור צעד לימוד קטן יותר המערכת כן מצליחה ללמוד.

כמו כן עבור קיבלנו תהליך התכנסות מהיר הרבה יותר ולמחיר נמוך יותר על פני . לכן נבחר את גודל הצעד להיות

האימון

נריץ את באלגוריתם עבור גודל צעד למשך 20 epochs.

png

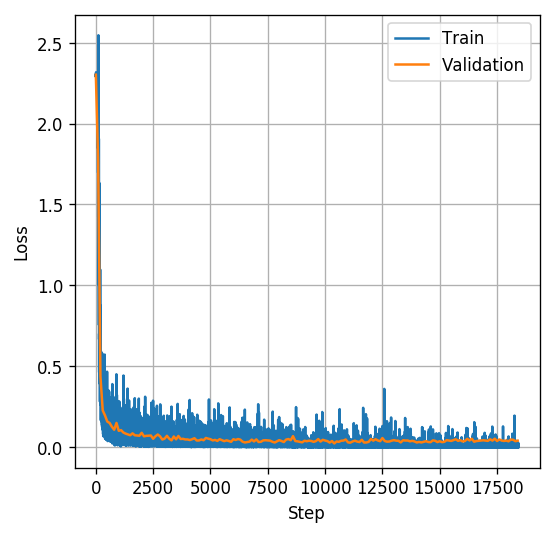
נראה שמודל התכנס יפה, משום שמחיר על סט הולידציה הגיע למישור. ניתן להניח שהמודל הגיע למינימום מקומי (אבל לא ניתן לדעת בוודאות)

הערכת ביצועים

נריץ את המודל לאחר הלימוד על סט המבחן ונקבל שפונקצית המחיר הינה

קיבלנו misclassification rate של כמעט אחוז בודד, כלומר שעבור אחוז מסט המבחן טעינו בחיזוי הסיפרה או לחילופין צדקנו ב99% מסט המבחן.

png

Attributions