תרגול 6
סיווג גנרטיבי

בעיית חיזוי - תזכורת

$\boldsymbol{X}$ - התצפיות/המדידות משתנה/וקטור אקראי אשר יש באפשרותינו למדוד.
$Y$ - התויות. משתנה אקראי אשר ברצונינו לחזות על סמך $X$ .
$\hat{y}=h\left(x\right)$ - פונקציית חיזוי של $Y$ כתלות ב $X$ .
$\ell\left(\hat{y},y\right)$ - פונקציית הפסד. ה”קנס” המתקבל בעבור חיזוי שגוי.
$R\left\lbrace h\right\rbrace=\mathbb{E}\left[\ell\left(h\left(X\right),Y\right)\right]$ - פנקציית הסיכון. התוחלת של ההפסד.

המטרה: למצוא פונקציית חיזוי אופטימאלית:

$h^*\left(x\right) = \underset{h}{\arg\min}\ R\left\lbrace h\right\rbrace= \underset{h}{\arg\min}\ \mathbb{E}\left[\ell\left(h\left(X\right),Y\right)\right]$

בעיית חיזוי - תזכורת - המשך

אנו מבחינים בין שני סוגי בעיות חיזוי:

סיווג: כאשר תחום הערכים של התוויות הינו דיסקרטי וסופי.
רגרסיה: כאשר תחום הערכים של התוויות הינו תחום רציף.

פונקציות הפסד נפוצות

הפסד אפס-אחד (zero-one loss)

$\ell\left(\hat{y},y\right) = I\left\lbrace \hat{y}\neq y\right\rbrace$

ההפסד הנפוץ בבעיות סיווג.
פונקציית הסיכון שלו נקראת: misclassification rate
החזאי האופטימאלי תחת הפסד זה הינו: $h\left(x\right)=\underset{y}{\arg\max}\quad p\left(y\lvert x\right)$

הפסד מרחק ריבועי ( $l_2$ loss)

$\ell\left(\hat{y},y\right) = \left(\hat{y}-y\right)^2$

ההפסד הנפוץ בבעיות רגרסיה.
פונקציית הסיכון שלו נקראת: Mean Square Error (MSE)
החזאי האופטימאלי תחת הפסד זה הינו משערך התוחלת המותנית: $h\left(x\right)=E\left[Y\lvert x\right]$

למידה מודרכת

בבעיות חיזוי שבהם אין אנו יודעים את הפילוג המשותף של $\boldsymbol{X}$ ו $Y$
יש ברשותינו מדגם של $N$ דיגימות משותפות שלהם: $D=\left\lbrace\boldsymbol{x}_i,y_i\right\rbrace$

גישה גנרטיבית

נשתמש במדגם על מנת לשערך את פונקציית הפילוג המשותפת $p_{\boldsymbol{X},Y}$
ובעזרת הפילוג המשותף נבנה את החזאי.

(שיטות אלו נקראות גנרטיביות משום שהם מנסות ללמוד את האופן שבו נוצר (generated) המדגם)

גישה גנרטיבית - המשך

נפרק לרוב את הפונקציית הצפיפות המושתפת באופן הבא:

$p_{\boldsymbol{X},Y}\left(\boldsymbol{x},y\right)=p_{\boldsymbol{X}\lvert Y}\left(\boldsymbol{x}\lvert y\right)p_Y\left(y\right)$

בבעיות סיווג $p_Y$ דיסקרטי וסופי.
ניתן לשערך אותו על פי: $p_Y\left(j\right)=\frac{1}{N}\sum_{i=1}^N I\left\lbrace y_i=j\right\rbrace$
את $p_{\boldsymbol{X}\lvert Y}$ נשערך בנפרד בעבור כל ערך של $Y$ .
זאת אומרת שאת $P\left(x\lvert Y=j\right)$ נשערך מתוך אוסף דגמים שמקיימות $y_i=j$ .

שיטות הסיווג הגנרטיביות נבדלות במודל של $p_{\boldsymbol{X}\lvert Y}$ , ואופן הלימוד שלו.

מסווג בייס נאיבי (Naïve Bayse Classifier)

ההנחה: הרכיבים של $\boldsymbol{X}$ הינם בלתי תלויים סטטיסטית.

תחת הנחה זו:

$p_{\boldsymbol{X}\lvert Y}\left(\boldsymbol{x}\lvert y\right)=\prod_{q=1}^d p_q\left(x_q\lvert y\right)$

את $p_q\left(x_q\lvert y\right)$ משערכים בעבור כל $Y$ וכל $q$ .

שיטה זו לא מגדירה כיצד ללמוד את הפילוגים החד מימדיים.
שיטה זו פותרת את בעיית הCurse of Dimenionality.
הנחת החוסר תלות בין הרכיבים לרוב רחוקה מלהיות נכונה.

Linear Discriminant Analysis (LDA)

הנחות:

$p_{\boldsymbol{X}\lvert Y}$ מפולגים נורמאלית.
לכל הפילוגים $p_{\boldsymbol{X}\lvert Y}$ אותה מטריצת covariance.

נניח כי $Y$ מקבל את סט הערכים $\left\lbrace1,\ldots,M\right\rbrace$ , ונשתמש בסימונים הבאים:

$G_j=\left\lbrace i:y_i=j\right\rbrace$ - תת-המדגם המקיים $y_i=j$ .
$\mu_j$ - התוחלות של הפילוגים הנורמאלים.
$\Sigma$ - מטריצת הcovariance של הפילוגים. (מטריצה אחת בעבור כל ה $N$ פילוגים).

שיערוך MLE של פרמטרי המודלים נותן:

$\boldsymbol{\mu}_j = \frac{1}{\left\lvert G_j\right\rvert}\sum_{i\in G_j}\boldsymbol{x}_i \\ \Sigma = \frac{1}{N}\sum_{i}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)^T$

Linear Discriminant Analysis (LDA) - המשך

הפרדה לינארית

בעבור המקרה של סיווג בינארי (סיווג לשני מחלקות) וzero-one loss מתקבל:

$h\left(x\right)= \begin{cases} 1\qquad \boldsymbol{a}^T \boldsymbol{x} + b > 0 \\ 0\qquad \text{otherwise}\\ \end{cases}$

כאשר:

$\boldsymbol{a}=\Sigma^{-1}\left(\boldsymbol{\mu}_1-\boldsymbol{\mu}_0\right) \\ b=\tfrac{1}{2}\left(\boldsymbol{\mu}_0^T\Sigma^{-1}\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1\right) + \log\left(\frac{p_Y\left(1\right)}{p_Y\left(0\right)}\right)$

נשים לב כי תנאי ההחלטה שבין שני התחומים הינו לינארי, ומכאן מקבל האלגוריתמם את שמו

Quadric Discriminant Analysis (QDA)

הנחות:

הפילוגים $p_{\boldsymbol{X}\lvert Y}$ הינם פילוגים נורמאלייים לכל ערך של $Y$ .

QDA דומה מאד לLDA רק ללא ההנחה השניה.

משערך MLE נותן:

$\boldsymbol{\mu}_j = \frac{1}{\left\lvert G_j\right\rvert}\sum_{i\in G_j}\boldsymbol{x}_i \\ \Sigma_j = \frac{1}{\left\lvert G_j\right\rvert}\sum_{i\in G_j}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_j\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_j\right)^T$

(כעת יש $\Sigma_j$ בעבור כל ערך של $Y$ , והוא מחושב על פי תת-המדגם $G_j$ המתאים.

משטח הפרדה ריבועי

בעבור המקרה של סיווג בינארי (סיווג לשני מחלקות) וzero-one loss מתקבל:

$h\left(x\right)= \begin{cases} 0\qquad \boldsymbol{x}^T C \boldsymbol{x} + \boldsymbol{a}^T \boldsymbol{x} + b > 0 \\ 1\qquad \text{otherwise}\\ \end{cases}$

כאשר:

$C=\tfrac{1}{2}\left(\Sigma_0^{-1}-\Sigma_1^{-1}\right) \\ \boldsymbol{a}=\Sigma_1^{-1}\boldsymbol{\mu}_1-\Sigma_0^{-1}\boldsymbol{\mu}_0 \\ b=\tfrac{1}{2}\left(\boldsymbol{\mu}_1^T\Sigma_1^{-1}\boldsymbol{\mu}_1 - \boldsymbol{\mu}_0^T\Sigma_0^{-1}\boldsymbol{\mu}_0\right) + \log\left(\frac{\left\lvert\Sigma_0\right\rvert^{1/2}p_Y\left(1\right)}{\left\lvert\Sigma_1\right\rvert^{1/2}p_Y\left(0\right)}\right)$

במקרה זה, משטח ההפרדה נתון על ידי פונקציה ריבועית ומכאן האלגוריתם מקבל את שמו.

תרגיל 6.1 - MAP

ביום טוב, עומרי כספי קולע בהסתברות $p$ מהקו. ביום רע, הוא קולע בהסתברות $q$ מהקו. $\alpha$ מהימים הם ימים טובים עבור עומרי.

ביום מסויים זרק עומרי $N$ זריקות וקלע $m$ מתוכם. מאמנו של עומרי צריך לזהות האם מדובר ביום טוב או רע של השחקן (ולהשאיר אותו או להחליף אותו בהתאמה).

מהו חוק ההחלטה אשר ממקסם את סיכויי המאמן לצדוק?

הניחו כי בהינתן המידע של האם יום מסויים הוא טוב או לא, ההסברות לקלוע זריקות שונות הינה הסתברות בלתי תלויה.

תרגיל 6.1 - MAP - פתרון

נגדיר את המשתנים האקראיים והפילוגים שלהם:

$X_i$ - האם קלע או לא. (0-החטיא, 1-קלע)
$Y$ - האם יום טוב או לא. (0-יום לא טוב, 1-יום טוב).

על פי הנתונים בשאלה:

$p\left(x_i\lvert Y=0\right)=\begin{cases} 1-q && x_i=0 \\ q && x_i=1 \\ \end{cases} \\ p\left(x_i\lvert Y=1\right)=\begin{cases} 1-p && x_i=0 \\ p && x_i=1 \\ \end{cases} \\ p\left(y\right)=\begin{cases} 1-\alpha && y=0 \\ \alpha && y=1 \\ \end{cases}$

תרגיל 6.1 - MAP - פתרון - המשך

בעיית MAP
$Y$ פרמטר בפילוג $X\lvert Y$ .
החזאי האופטימאלי של $Y$ הינו:

$\begin{aligned} \hat{y} & = \underset{y}{\arg\max}\quad p\left(y \lvert \left\lbrace x_i\right\rbrace\right) \\ & = \underset{y}{\arg\max}\quad p\left(\left\lbrace x_i\right\rbrace \lvert y\right)p\left(y\right) \\ & = \underset{y}{\arg\max}\quad \left(\prod_{i=1}^d p\left(x_i \lvert y\right)\right)p\left(y\right) \\ \end{aligned}$

בעבור $y=0$ נקבל:

$\left(\prod_{i=1}^d p\left(x_i \lvert y\right)\right)p\left(y\right) = q^m\left(1-q\right)^{N-m}\left(1-\alpha\right)$

בעבור $y=1$ נקבל:

$\left(\prod_{i=1}^d p\left(x_i \lvert y\right)\right)p\left(y\right) = p^m\left(1-p\right)^{N-m}\alpha$

תרגיל 6.1 - MAP - פתרון - המשך 2

בעבור $y=0$ נקבל:

$\left(\prod_{i=1}^d p\left(x_i \lvert y\right)\right)p\left(y\right) = q^m\left(1-q\right)^{N-m}\left(1-\alpha\right)$

בעבור $y=1$ נקבל:

$\left(\prod_{i=1}^d p\left(x_i \lvert y\right)\right)p\left(y\right) = p^m\left(1-p\right)^{N-m}\alpha$

לכן החיזוי האופטימאלי יהיה:

$\begin{aligned} \hat{y} & = \begin{cases} 0 && q^m\left(1-q\right)^{N-m}\left(1-\alpha\right) > p^m\left(1-p\right)^{N-m}\alpha \\ 1 && \text{otherwise} \end{cases} \\ & = \begin{cases} 0 && \left(\frac{q}{p}\right)^m\left(\frac{1-q}{1-p}\right)^{N-m}\frac{1-\alpha}{\alpha} > 1 \\ 1 && \text{otherwise} \end{cases} \\ \end{aligned}$

תרגיל 6.2

בסוואנה חיים שלושה זני פילים אשר נמצאים בסכנת הכחדה. ידוע כי כל אחד משלושת הזנים ניזון מצמחיה מעט שונה ועל מנת לשמר את אוכלוסיית הפילים מעוניינים לפזר להם אוכל ברחבי הסוואנה. בכדי למקסם את האפקטיביות של פעולה זו מעוניינים לשערך בכל נקודת חלוקה מהו הזן שהכי סביר להמצא באותה נקודה על מנת להתאים את סוג המזון לזן זה.

הפילוג של זני הפילים על פני הסוואנה אינו ידוע אך נתונות לנו התצפית הבאה של הקואורדינטות בהם נצפו הפילים:

Type	X_1	X_2
1	1	2
1	3	2
2	-2	2
3	0	-1
3	0	-5

השתמש במסווג LDA על מנת לבנות חזאי אשר ישערך את הזן הזפוץ ביותר בכל קואורדינטה.

תרגיל 6.2 - פתרון

Type	X_1	X_2
1	1	2
1	3	2
2	-2	2
3	0	-1
3	0	-5

סימונים:

$\boldsymbol{x}_i$ הקאורדינטה. לדוגמא: $\boldsymbol{x}_4=\begin{pmatrix}0 & -1\end{pmatrix}^T$
$y_i$ הזן. לדוגמא: $y_4=3$
$G_j$ אוסף כל התצפיות של שבהם הזן הוא $j$ . לדוגמא: $G_3=\left\lbrace 4,5\right\rbrace$

תרגיל 6.2 - פתרון - המשך

Type	X_1	X_2
1	1	2
1	3	2
2	-2	2
3	0	-1
3	0	-5

נחשב את הפילוג הא-פריורי של כל אחד מן הזנים:

$p_Y\left(1\right)=\frac{\left\lvert G_1\right\rvert}{N}=\frac{2}{5} \\ p_Y\left(2\right)=\frac{\left\lvert G_2\right\rvert}{N}=\frac{1}{5} \\ p_Y\left(3\right)=\frac{\left\lvert G_3\right\rvert}{N}=\frac{2}{5}$

תרגיל 6.2 - פתרון - המשך 2

Type	X_1	X_2
1	1	2
1	3	2
2	-2	2
3	0	-1
3	0	-5

נחשב את הפרמטרים של שלושת הפילוגים הנורמאלים:

$\boldsymbol{\mu}_1 =\frac{1}{\left\lvert G_1\right\rvert}\sum_{i\in G_1}\boldsymbol{x}_i =\frac{1}{2}\left(\begin{pmatrix}1\\2\end{pmatrix}+\begin{pmatrix}3\\2\end{pmatrix}\right) =\begin{pmatrix}2\\2\end{pmatrix}\\ \boldsymbol{\mu}_2 =\frac{1}{\left\lvert G_2\right\rvert}\sum_{i\in G_2}\boldsymbol{x}_i =\begin{pmatrix}-2\\2\end{pmatrix}\\ \boldsymbol{\mu}_3 =\frac{1}{\left\lvert G_3\right\rvert}\sum_{i\in G_3}\boldsymbol{x}_i =\frac{1}{2}\left(\begin{pmatrix}0\\-1\end{pmatrix}+\begin{pmatrix}0\\-5\end{pmatrix}\right) =\begin{pmatrix}0\\-3\end{pmatrix}\\$

תרגיל 6.2 - פתרון - המשך 3

נחשב את מטריצת covariance המשותפת של הפילוגים:

$\Sigma=\frac{1}{N}\sum_{i}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)^T$

דרך נוחה לחשב את הסכום בביטוי זה הינה באופן הבא. נגדיר את המטריצה של התצפיות לאחר חיסור של התוחלת המתאימה לכל זן:

$\tilde{X} =\begin{pmatrix}-\boldsymbol{x}_1-\\-\boldsymbol{x}_2-\\-\boldsymbol{x}_3-\\-\boldsymbol{x}_4-\\-\boldsymbol{x}_5-\end{pmatrix}-\begin{pmatrix}-\boldsymbol{\mu}_{y_1}-\\-\boldsymbol{\mu}_{y_2}-\\ -\boldsymbol{\mu}_{y_3}\\-\boldsymbol{\mu}_{y_4}-\\-\boldsymbol{\mu}_{y_5}-\end{pmatrix} =\begin{pmatrix}-1 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 2 \\ 0 & -2 \end{pmatrix}$

תרגיל 6.2 - פתרון - המשך 4

ניתן להראות בקלות כי ניתן לכתוב את הסכום בביטוי ל $\Sigma$ באופן הבא:

$\begin{aligned} \Sigma & =\frac{1}{N}\sum_{i}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)^T=\frac{1}{N}\tilde{X}^T\tilde{X}\\ & =\frac{1}{5}\begin{pmatrix}-1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 & -2 \end{pmatrix}\begin{pmatrix}-1 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 2 \\ 0 & -2 \end{pmatrix} \\ & =\frac{1}{5}\begin{pmatrix} 2 & 0 \\ 0 & 8 \end{pmatrix} \end{aligned}$

תרגיל 6.2 - פתרון - המשך 5

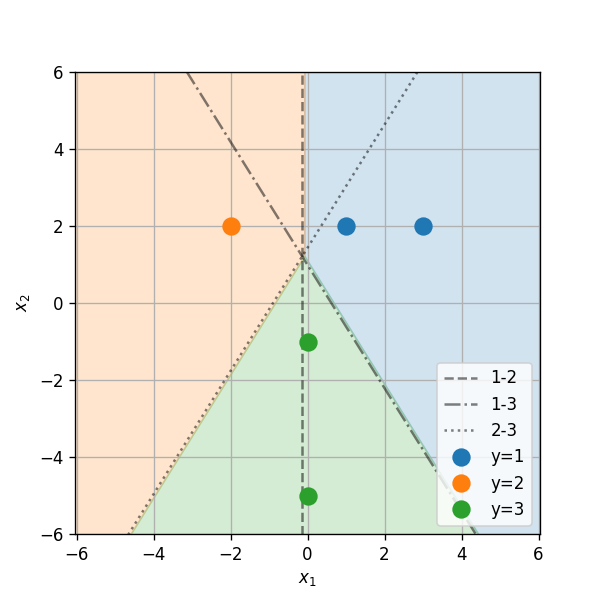
נשתמש כעת בפילוגים שאותם שיערכנו על מנת לבנות את החזאי. האיזור שבו זן 1 הינו הזן הסביר ביותר הינו האיזור שבו מתקיים:

$\begin{cases} p_{Y\lvert X}\left(1\lvert x\right) > p_{Y\lvert X}\left(2\lvert x\right) \\ p_{Y\lvert X}\left(1\lvert x\right) > p_{Y\lvert X}\left(3\lvert x\right) \end{cases}$

נחשב את התנאי הראשון

$\begin{aligned} p_{Y\lvert X}\left(1\lvert x\right)&> p_{Y\lvert X}\left(2\lvert x\right) \\ \Leftrightarrow p_{X\lvert Y}\left(x\lvert 1\right)p_Y\left(1\right)&> p_{X\lvert Y}\left(x\lvert 2\right)p_Y\left(2\right) \\ \Leftrightarrow e^{-\tfrac{1}{2}\left(x-\mu_1\right)^T\Sigma^{-1}\left(x-\mu_1\right)}p_Y\left(1\right)&>e^{-\tfrac{1}{2}\left(x-\mu_2\right)^T\Sigma^{-1}\left(x-\mu_2\right)}p_Y\left(2\right) \\ \end{aligned} \\ \Leftrightarrow x^T\Sigma^{-1}\left(\mu_1-\mu_2\right)+\tfrac{1}{2}\left(\mu_2^T\Sigma^{-1}\mu_2 -\mu_1^T\Sigma^{-1}\mu_1\right)+\log\left(\frac{p_Y\left(1\right)}{p_Y\left(2\right)}\right)>0\\$

תרגיל 6.2 - פתרון - המשך 6

$\Leftrightarrow x^T\Sigma^{-1}\left(\mu_1-\mu_2\right)+\tfrac{1}{2}\left(\mu_2^T\Sigma^{-1}\mu_2 -\mu_1^T\Sigma^{-1}\mu_1\right)+\log\left(\frac{p_Y\left(1\right)}{p_Y\left(2\right)}\right)>0\\$

זוהי למעשה הפרדה לשני תחומים על ידי הקו הבא:

$\boldsymbol{a}^T \boldsymbol{x}+b=0$

כאשר:

$\boldsymbol{a}=\Sigma^{-1}\left(\boldsymbol{\mu}_1-\boldsymbol{\mu}_2\right) =\begin{pmatrix} 10 \\ 0 \end{pmatrix} \\ b=\tfrac{1}{2}\left(\boldsymbol{\mu}_2^T\Sigma^{-1}\boldsymbol{\mu}_2 - \boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1\right) + \log\left(\frac{p_Y\left(1\right)}{p_Y\left(2\right)}\right) =\log\left(2\right)$

מכאן שהקו המפריד בין זן 1 ל זן 2 נתון על ידי:

$1-2:\quad 10x_1+\log\left(2\right)=0$

תרגיל 6.2 - פתרון - המשך 7

באופן דומה ניתן לחשב גם את שני קווי ההפרדה האחרים (בין 1 ל 3 ובין 2 ל 3):

$\begin{aligned} 1-2: & \quad 10x_1+\log\left(2\right)=0 \\ 1-3: & \quad 5x_1+\frac{25}{8}x_2+\frac{55}{16}=0 \\ 2-3: & \quad -5x_1+\frac{25}{8}x_2+\frac{55}{16}-\log\left(2\right)=0 \end{aligned}$

elephants classification

בעיה מעשית

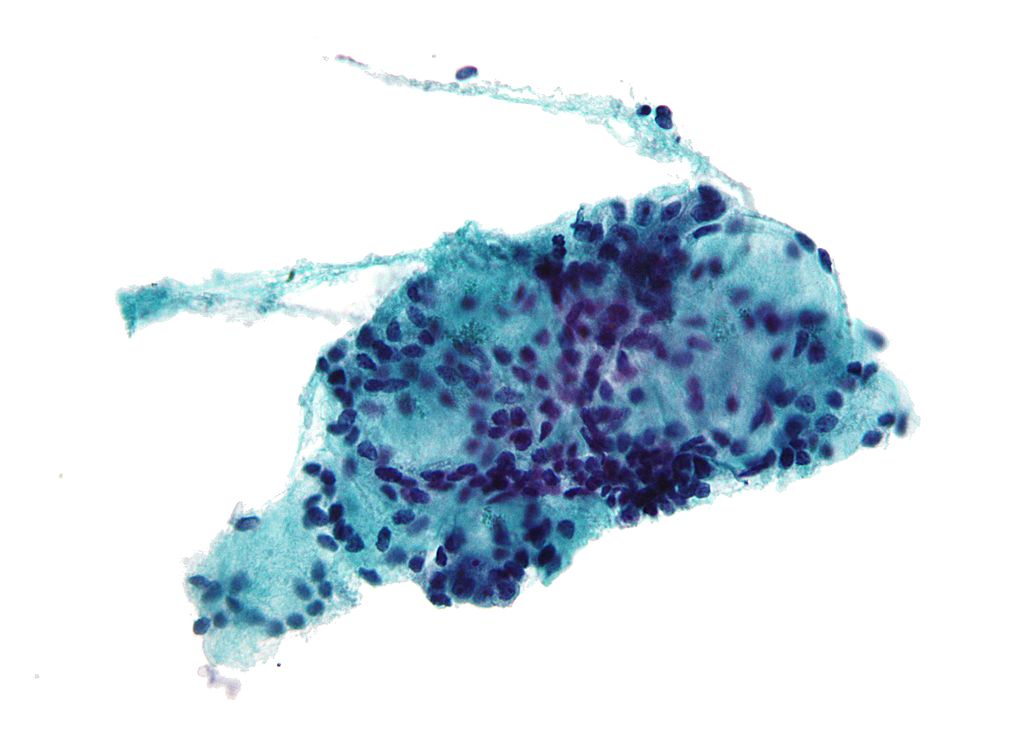
המדגם: Breast Cancer Wisconsin

נעבוד שוב עם המדגם של דגימות התא לאבחון סרטן שד. (את המדגם המקורי ניתן למצוא פה, בקורס נעבוד עם הגרסא הזו)

השדות במדגם

להלן 10 השורות הראשונות במדגם:

	id	diagnosis	radius_mean	texture_mean	perimeter_mean	area_mean	smoothness_mean	compactness_mean	concavity_mean	concave points_mean	...	radius_worst	texture_worst	perimeter_worst	area_worst	smoothness_worst	compactness_worst	concavity_worst	concave points_worst	symmetry_worst	fractal_dimension_worst
0	842302	M	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	...	25.38	17.33	184.60	2019.0	0.1622	0.6656	0.7119	0.2654	0.4601	0.11890
1	842517	M	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	...	24.99	23.41	158.80	1956.0	0.1238	0.1866	0.2416	0.1860	0.2750	0.08902
2	84300903	M	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	...	23.57	25.53	152.50	1709.0	0.1444	0.4245	0.4504	0.2430	0.3613	0.08758
3	84348301	M	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	...	14.91	26.50	98.87	567.7	0.2098	0.8663	0.6869	0.2575	0.6638	0.17300
4	84358402	M	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	...	22.54	16.67	152.20	1575.0	0.1374	0.2050	0.4000	0.1625	0.2364	0.07678
5	843786	M	12.45	15.70	82.57	477.1	0.12780	0.17000	0.15780	0.08089	...	15.47	23.75	103.40	741.6	0.1791	0.5249	0.5355	0.1741	0.3985	0.12440
6	844359	M	18.25	19.98	119.60	1040.0	0.09463	0.10900	0.11270	0.07400	...	22.88	27.66	153.20	1606.0	0.1442	0.2576	0.3784	0.1932	0.3063	0.08368
7	84458202	M	13.71	20.83	90.20	577.9	0.11890	0.16450	0.09366	0.05985	...	17.06	28.14	110.60	897.0	0.1654	0.3682	0.2678	0.1556	0.3196	0.11510
8	844981	M	13.00	21.82	87.50	519.8	0.12730	0.19320	0.18590	0.09353	...	15.49	30.73	106.20	739.3	0.1703	0.5401	0.5390	0.2060	0.4378	0.10720
9	84501001	M	12.46	24.04	83.97	475.9	0.11860	0.23960	0.22730	0.08543	...	15.09	40.68	97.65	711.4	0.1853	1.0580	1.1050	0.2210	0.4366	0.20750

במדגם 569 שורות (דגימות).

לשם הפשטות (וויזואליזציה) אנו נעבוד תחילה רק עם התווית ושני השדות הבאים:

diagnosis - התווית של הדגימה: M = malignant (סרטני), B = benign (בריא)
radius_mean - רדיוס התא הממוצע בדגימה
texture_mean - סטיית התקן הממוצעת של רמת האפור בצבע של כל תא בדגימה.

(בהמשך נעבוד עם יתר השדות)

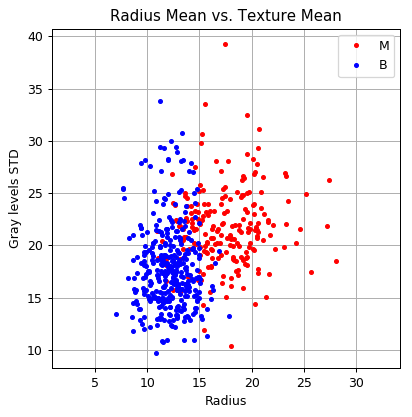
השדות במדגם - המשך

הפילוג של נתונים אלו נראה כך:

Raw data

תזכורת לבעיה: חיזוי האם תא הינו סרטני או לא

אנו מעוניינים לעזור לצוות הרפואי לבצע אבחון נכון של דגימות לדגימות סרטניות (malignant) או בריאות (benign) על סמך הנתונים המספריים שמחושבים לכל דגימה.

באופן פורמאלי:

$X=\left[\text{mean_radius},\text{mean_texture}\right]^T$ - ערכי התצפית של דגימה מסויימת.
$Y$ - התווית הבינארית של האם הדגימה סרטנית או לא. (0-בריא, 1-סרטני)

נהיה מעוניינים למצוא את פונקציית החיזוי אשר ממזערת את:

$R\left\lbrace h\right\rbrace=E\left[I\left\lbrace h\left(\boldsymbol{X}\right)\neq Y\right\rbrace\right]$

(zero-one loss)

הפרשה של סט בחן

לשם שיערוך ביצועיו של החזאי נפריש 20% מהמדגם לסט בחן (test set).

(במודלים שאיתם נעבוד בתרגול זה אין hyper-parameters ולכן לא יהיה לנו צורך בסט אימות (validataion set))

שיטה 1: LDA.

נבנה חזאי על ידי שימוש בLDA.

$p_Y\left(j\right)=\frac{1}{N}\sum_{i=1}^N I\left\lbrace y_i=0\right\rbrace,\quad j\in\left(\lbrace 0,1\right\rbrace \\ \boldsymbol{\mu}_j = \frac{1}{\left\lvert G_j\right\rvert}\sum_{i\in G_j}\boldsymbol{x}_i \\ \Sigma = \frac{1}{N}\sum_{i}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_{y_i}\right)^T$

שיטה 1: LDA - המשך

החזאי המקבל הינו:

$h\left(x\right)= \begin{cases} 1\qquad \boldsymbol{a}^T \boldsymbol{x} + b > 0 \\ 0\qquad \text{otherwise}\\ \end{cases}$

כאשר:

שיטה 1: LDA - המשך 2

נשרטט את הפילוגים הנורמאלים המתקבלים ואת קו ההפרדה הליניארי על גבי הנתונים:

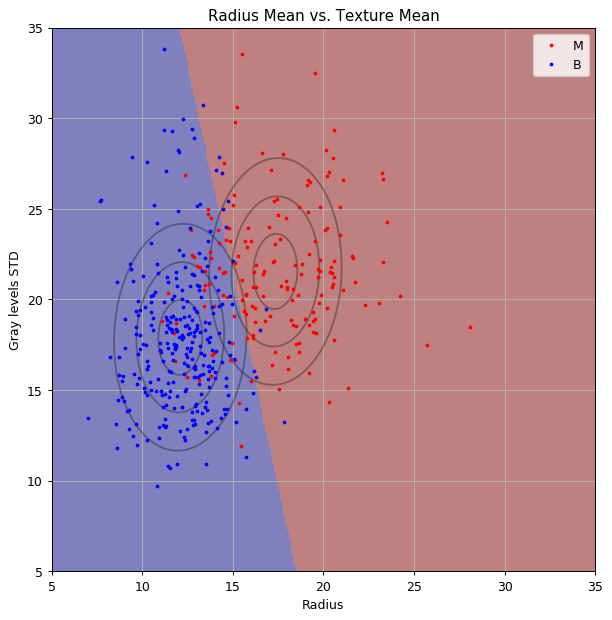
LDA results

שיטה 1: LDA - המשך 3

הערכת ביצועים

נשערך את ביצועי החזאי על ידי חישוב הסיכון האמפירי המתקבל על סט הבחן.

$\hat{R}\left\lbrace h\right\rbrace=\frac{1}{N}\sum_{i=1}^N I\left\lbrace h\left(\boldsymbol{x}_i\right)\neq y_i\right\rbrace$

הסיכון המשוערך המתקבל הינו: 0.096

✍️ תרגיל 6.3

א) הציעו שיטה להעריך את מידת הודאות של החיזוי על סמך המודל שקיבלנו.

ב) כיצד היה משתנה החזאי במידה והיינו יודעים כי הסיכוי הא-פריוירי של דגימה להיות סרטנית הינה 5% (ולא כמו הפילוג המופיע במדגם)

✍️ תרגיל 6.3 א

הציעו שיטה להעריך את מידת הודאות של החיזוי על סמך המודל שקיבלנו.

פתרון

אלגוריתם גנרטיבי -> שיערכנו מודל ההסתברותי המלא ->
נוכל לשערך את ההסתברות לקבל תווית מסויימת בהניתן התצפיות.

הסיכוי של דגימה נתונה להיות סרטנית נתון על ידי:

$p_{Y\lvert \boldsymbol{X}}\left(1\lvert\boldsymbol{x}\right) = \frac{p_{\boldsymbol{X}\lvert Y}\left(\boldsymbol{x}\lvert 1\right)p_Y\left(1\right)}{p_{\boldsymbol{X}\lvert Y}\left(\boldsymbol{x}\lvert 0\right)p_Y\left(0\right)+p_{\boldsymbol{X}\lvert Y}\left(\boldsymbol{x}\lvert 1\right)p_Y\left(1\right)} \\$

כאשר:

$p_{\boldsymbol{X}\lvert Y}\left(\boldsymbol{x}\lvert j\right)=\frac{1}{2\pi\left\lvert\Sigma\right\rvert}\exp\left(-\tfrac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_j\right)^T\Sigma^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_j\right)\right)$
$\mu_j$ , $\Sigma$ ו $p_Y\left(j\right)$ הם הפרמטרים שכבר שיערכנו.

✍️ תרגיל 6.3 ב

כיצד היה משתנה החזאי במידה והיינו יודעים כי הסיכוי הא-פריוירי של דגימה להיות סרטנית הינה 5% (ולא כמו הפילוג המופיע במדגם)

פתרון

נוכל להשתמש בפילוג הידוע של $p_Y$ במקום לשערך אותו. (כל שאר החישוב יהיה זהה).

במקרה של LDA, פילוג זה מופיע רק באיבר $b$ של פונקצייית החיזוי, אשר מגדיר את המיקום של משטח ההפרדה.

$b=\tfrac{1}{2}\left(\boldsymbol{\mu}_0^T\Sigma^{-1}\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1^T\Sigma^{-1}\boldsymbol{\mu}_1\right) + \log\left(\frac{p_Y\left(1\right)}{p_Y\left(0\right)}\right)$

נשתמש כעת ב:

$p_Y\left(y\right)=\begin{cases} 0.95 & y=0 \\ 0.05 & y=1 \\ \end{cases}$

✍️ תרגיל 6.3 ב - המשך

ונקבל את פונקציית החיזוי הבאה:

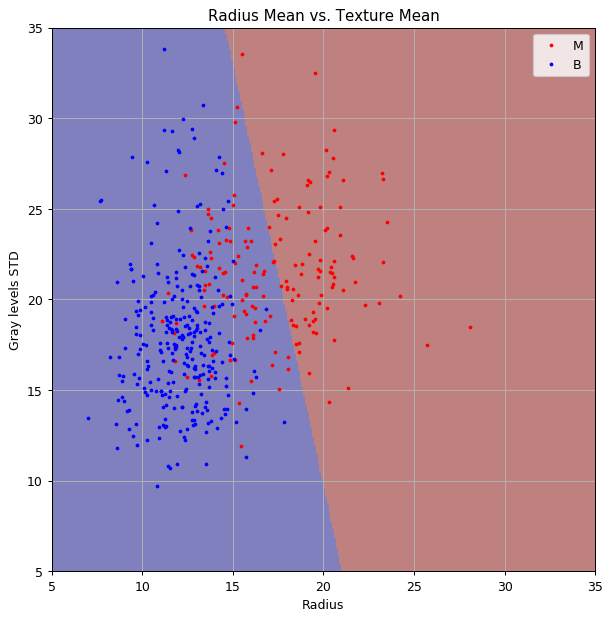
LDA results with prior

קו ההפרדה זז לימין.

הפילוג הא-פריורי מקטין את ההסתברות שדגימה מסויימת הינה סרטנית, שמתבטא באופן דומה גם בסיכוי הפוסטריורי. לכן איזור גדול יותר ממופה כעת לתווית של “לא סרטני”.

שיטה 2: QDA

נבנה חזאי על ידי שימוש בQDA.

נחשב מטריצת covariance בעבור כל אחת מהתוויות בנפרד (שאר הפרמטרים לא משתנים).

$\Sigma_j = \frac{1}{\left\lvert G_j\right\rvert}\sum_{i\in G_j}\left(\boldsymbol{x}_i-\boldsymbol{\mu}_j\right)\left(\boldsymbol{x}_i-\boldsymbol{\mu}_j\right)^T$

החזאי המקבל הינו:

$h\left(x\right)= \begin{cases} 0\qquad \boldsymbol{x}^T C \boldsymbol{x} + \boldsymbol{a}^T \boldsymbol{x} + b > 0 \\ 1\qquad \text{otherwise}\\ \end{cases}$

כאשר:

שיטה 2: QDA - המשך

נשרטט את הפילוגים הנורמאלים המתקבלים ואת קו ההפרדה על גבי הנתונים:

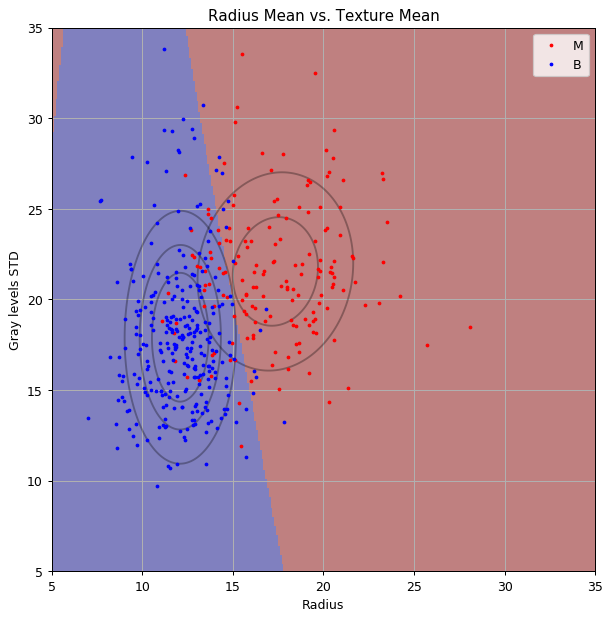
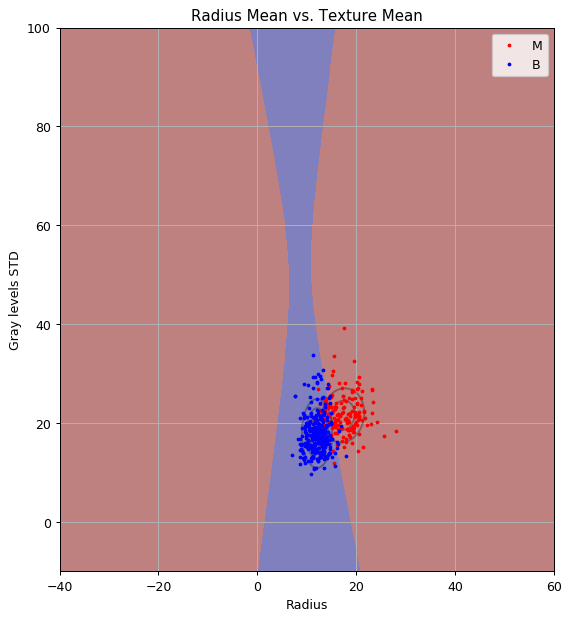
QDA results

הסיכון המשוערך על סט הבחן הינו: 0.088 (קיבלנו שיפור קל בביצועים)

הגדלת כמות השדות בוקטור התצפיות

נחזור על תהליך של חיזוי בשיטת QDA כאשר אנו לוקחים בכל פעם את $m$ השדות הראשונים במדגם.

נשרטט את הסיכון המתקבל על סט האימון ועל סט הבחן כתלות ב $m$ :

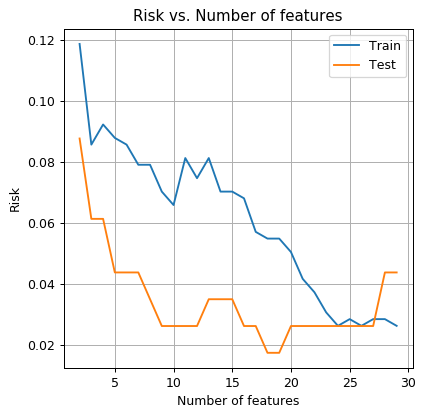
Risk vs. number of features

תרגיל 6.4

Risk vs. number of features

כיצד תסבירו את העובדה כי מנקודה מסויימת הסיכון על סט הבחן הולך ונעשה גרוע ככל שאנו מגדילים את כמות השדות? מהי כמות הפרמטרים במודל כתלות ב $m$ (מספר השדות)? מה גודלו של סט האימון?

הציעו מניפולציה אותה ניתן לעשות למדגם על מנת לבנות חזאי אשר כן משתמש במידע מכל השדות אך עם מספר פרמטרים מוגבל.

תרגיל 6.4 - פתרון

זוהי דוגמא קלסית להתאמת יתר (overfitting).
ככל שמספר השדות גדל, מספר הפרמטרים של המודל גדל והמודל יכול לייצג תלויות יותר ויותר מורכבות.
בQDA מספר הפרמטרים הינו בערך $m^2$ , במקרה של 30 שדות יש במודל בערך 900 פרמטרים בעוד שסט האימון יש $80%\cdot596=455$ דגימות.
ככלל אצבע, נרצה לרוב שמספר הפרמטרים במודל שלנו יהיה קטן בלפחות סדר גודל אחד ממספר הדגמים בסט האימון (נכון חלקית).

דרך אחת להתמודד עם בעיה זו הינה לבצע הורדת מימד לוקטור התצפיות בשיטות כגון PCA.

תרגיל 6.6 - פונקציית הפסד לא סימטרית

נסתכל על בעיית החיזוי הבאה.

ידוע הפילוג המשותף של שני משתנים אקראיים $X$ ו $Y$ , כאשר $Y$ הוא משתנה בינארי. כמו כן נתונה לנו פונקציית ההפסד הבאה:

$l\left(y,\hat{y}\right)=\begin{cases} 1 & y=0,\hat{y}=1 \\ \alpha & y=1,\hat{y}=0 \\ 0 & \text{otherwise} \end{cases}.$

מצאו ביטוי לחזאי האופטימאלי של $Y$ בהינתן $X$ אשר ממזער את פונקציית הסיכון המתאימה לפונקציית ההפסד הנתונה.

תרגיל 6.6 - פונקציית הפסד לא סימטרית - המשך

$l\left(y,\hat{y}\right)=\begin{cases} 1 & y=0,\hat{y}=1 \\ \alpha & y=1,\hat{y}=0 \\ 0 & \text{otherwise} \end{cases}.$

פתרון

$\begin{aligned} h^*\left(x\right) & = \underset{\hat{y}}{\arg\min}\quad \mathbb{E}\left[l\left(Y,\hat{y}\right)\lvert X=x\right] \\ & = \underset{\hat{y}}{\arg\min}\quad p_{Y\lvert X}\left(0\lvert x\right)l\left(0,\hat{y}\right)+p_{Y\lvert X}\left(1\lvert x\right)l\left(1,\hat{y}\right) \\ \end{aligned}$

בעבור $\hat{y}=0$ נקבל:

$p_{Y\lvert X}\left(0\lvert x\right)l\left(0,0\right)+p_{Y\lvert X}\left(1\lvert x\right)l\left(1,0\right)=\alpha p_{Y\lvert X}\left(1\lvert x\right)$

ובעבור $\hat{y}=1$ נקבל:

$p_{Y\lvert X}\left(0\lvert x\right)l\left(0,1\right)+p_{Y\lvert X}\left(1\lvert x\right)l\left(1,1\right)=p_{Y\lvert X}\left(0\lvert x\right)$

תרגיל 6.6 - פונקציית הפסד לא סימטרית - המשך 2

$l\left(y,\hat{y}\right)=\begin{cases} 1 & y=0,\hat{y}=1 \\ \alpha & y=1,\hat{y}=0 \\ 0 & \text{otherwise} \end{cases}.$

פתרון

מכאן שהחזאי האופטימאלי יהיה:

$\begin{aligned} h^*\left(x\right) & = \begin{cases} 0 & \alpha p_{Y\lvert X}\left(1\lvert x\right) < p_{Y\lvert X}\left(0\lvert x\right) \\ 1 & \text{otherwise} \end{cases} \\ & = \begin{cases} 0 & \frac{p_{Y\lvert X}\left(0\lvert x\right)}{p_{Y\lvert X}\left(1\lvert x\right)}>\alpha \\ 1 & \text{otherwise} \end{cases} \end{aligned}$

תרגול 6סיווג גנרטיבי

בעיית חיזוי - תזכורת

בעיית חיזוי - תזכורת - המשך

פונקציות הפסד נפוצות

הפסד אפס-אחד (zero-one loss)

הפסד מרחק ריבועי (l_2 loss)

למידה מודרכת

גישה גנרטיבית

גישה גנרטיבית - המשך

מסווג בייס נאיבי (Naïve Bayse Classifier)

Linear Discriminant Analysis (LDA)

Linear Discriminant Analysis (LDA) - המשך

הפרדה לינארית

Quadric Discriminant Analysis (QDA)

משטח הפרדה ריבועי

תרגיל 6.1 - MAP

תרגיל 6.1 - MAP - פתרון

תרגיל 6.1 - MAP - פתרון - המשך

תרגיל 6.1 - MAP - פתרון - המשך 2

תרגיל 6.2

תרגיל 6.2 - פתרון

תרגיל 6.2 - פתרון - המשך

תרגיל 6.2 - פתרון - המשך 2

תרגיל 6.2 - פתרון - המשך 3

תרגיל 6.2 - פתרון - המשך 4

תרגיל 6.2 - פתרון - המשך 5

תרגיל 6.2 - פתרון - המשך 6

תרגיל 6.2 - פתרון - המשך 7

בעיה מעשית

המדגם: Breast Cancer Wisconsin

השדות במדגם

השדות במדגם - המשך

תזכורת לבעיה: חיזוי האם תא הינו סרטני או לא

הפרשה של סט בחן

שיטה 1: LDA.

שיטה 1: LDA - המשך

שיטה 1: LDA - המשך 2

שיטה 1: LDA - המשך 3

הערכת ביצועים

✍️ תרגיל 6.3

✍️ תרגיל 6.3 א

פתרון

✍️ תרגיל 6.3 ב

פתרון

✍️ תרגיל 6.3 ב - המשך

שיטה 2: QDA

שיטה 2: QDA - המשך

הגדלת כמות השדות בוקטור התצפיות

תרגיל 6.4

תרגיל 6.4 - פתרון

תרגיל 6.6 - פונקציית הפסד לא סימטרית

תרגיל 6.6 - פונקציית הפסד לא סימטרית - המשך

פתרון

תרגיל 6.6 - פונקציית הפסד לא סימטרית - המשך 2

פתרון

תרגול 6
סיווג גנרטיבי

הפסד מרחק ריבועי ( $l_2$ loss)