תרגול 4
K-Means

תיאוריה -אשכול

המטרה

לחלק אוסף של פרטים לקבוצות המכונים אשכולות (clusters)

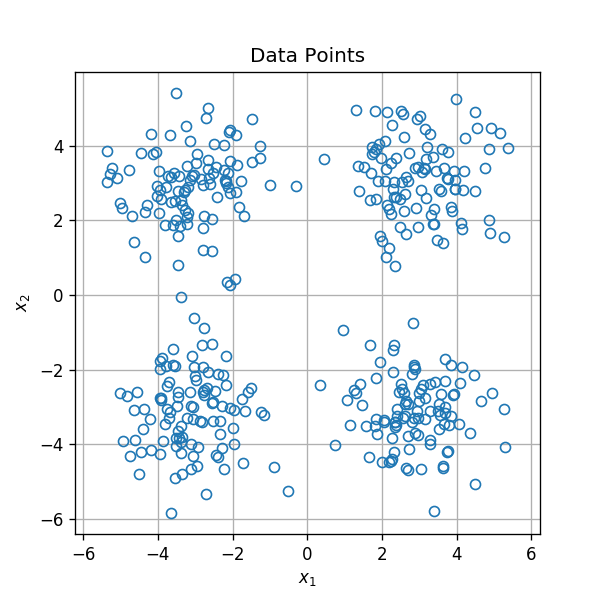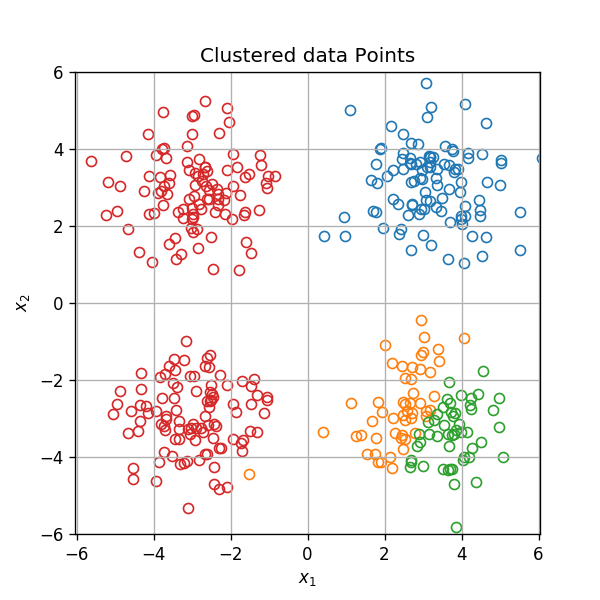
normal ⇦ normal

דוגמאות

לבצע הנחות על פרט על סמך פרט אחר באשכול.

לדוגמא: להציע בחנות אינטרנט מוצרים על סמך לקוחות אחרים.
לתת טיפול שונה לכל אשכול.

לדוגמא: משרד ממשלתי שרוצה להפנות קבוצות שונות באוכלוסיה לערוצי מתן שירות שונים

אלגוריתמי אשכול שונים

ישנם מספר רב של דרכים לבצע אישכול לאוסף של נתונים

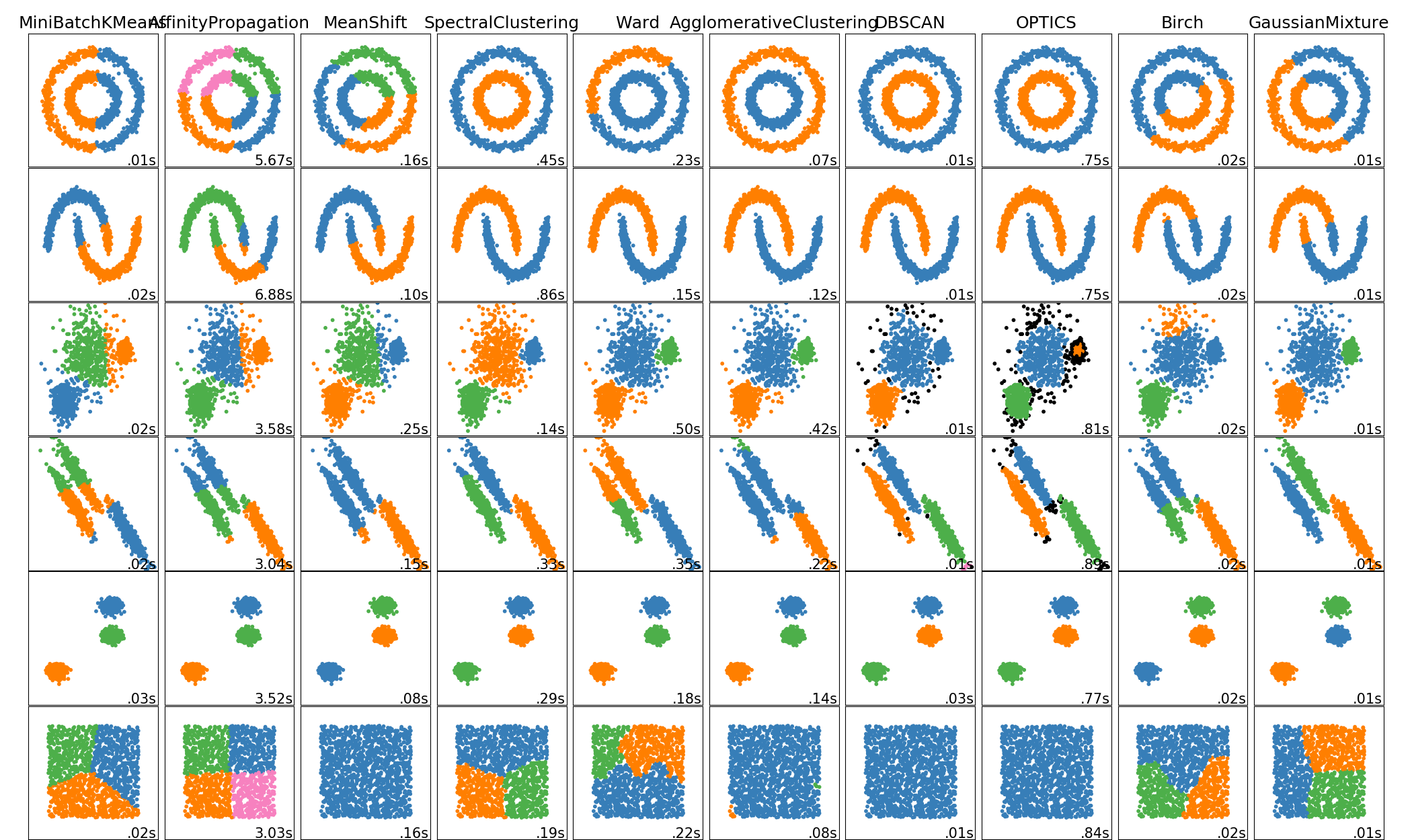
scikit-learn's clustering

לרוב נעבוד עם נתונים ממימד גבוה, ולא נוכל לצייר את האשכולות.

האלגוריתם K-means

סימונים:

$K$ - מספר האשכולות (גודל אשר נקבע מראש).
$G_i$ - אוסף האינדקסים של האשכול ה- $i$ . לדוגמא: $G_5=\left\lbrace3, 6, 9, 13\right\rbrace$
$\left\lvert G_i\right\rvert$ - גודל האשכול ה- $i$ (מספר הפרטים בקבוצה)
$\left\lbrace G_i\right\rbrace$ - חלוקה מסויימת לאשכולות
$\left\lbrace G_i\right\rbrace^*$ - החלוקה האופטימאלית (תחת קריטריון מסויים)

מנסה למזער את המרחק הריבועי הממוצע בין וקטור לבין שאר חברי האשכול שלו:

$\underset{\left\{G_i\right\}}{\arg\min}\sum_{i=1}^K\frac{1}{\left\lvert G_i\right\rvert}\sum_{j,k\in S_i}\left\lVert \boldsymbol{x}_j-\boldsymbol{x}_k \right\rVert^2$

האלגוריתם K-means

הבעיה השקולה

מרכז המסה (center of mass or centroid) או המרכז של אשכול:

$\boldsymbol{\mu}_i=\frac{1}{\left\lvert G_i\right\rvert}\sum_{\boldsymbol{x}\in G_i}\boldsymbol{x}$

בעיית האופטימיזציה שקולה לבעיה של מיזעור המרחק הריבועי בין וקטור למרכז המסה של האשכול שלו:

$\underset{\left\{G_i\right\}}{\arg\min}\sum_{i=1}^K\sum_{j\in G_i}\left\lVert \boldsymbol{x}_j-\boldsymbol{\mu}_i \right\rVert^2$

האלגוריתם K-means

שלבי האלגוריתם

איתחול: $t=0$ , בחירת $K$ מרכזי אשכולות $\left\lbrace \mu_i^{\left(0\right)} \right\rbrace_{i=1}^K$
חזרה עד להתכנסות ():
- שיוך כל נקודה לאשכול, על פי המרכז הקרוב עליו ביותר:
  $G_i^{\left(t\right)}=\left\lbrace j: \left\lVert\boldsymbol{x}_j-\boldsymbol{\mu}_i^{\left(t\right)}\right\rVert^2<\left\lVert\boldsymbol{x}_j-\boldsymbol{\mu}_l^{\left(t\right)}\right\rVert^2 \quad\forall l\neq i\right\rbrace$
  (במקרה של שני מרכזים במרחק זהה נבחר בזה בעל האינדקס הנמוך יותר).
- עדכון מרכזי האשכולות על פי: $\boldsymbol{\mu}_i^{\left(t+1\right)}=\frac{1}{\left\lvert G_i^{\left(t\right)}\right\rvert}\sum_{\boldsymbol{x}\in G_i^{\left(t\right)}}\boldsymbol{x}$
- קידום: $t\leftarrow t+1$

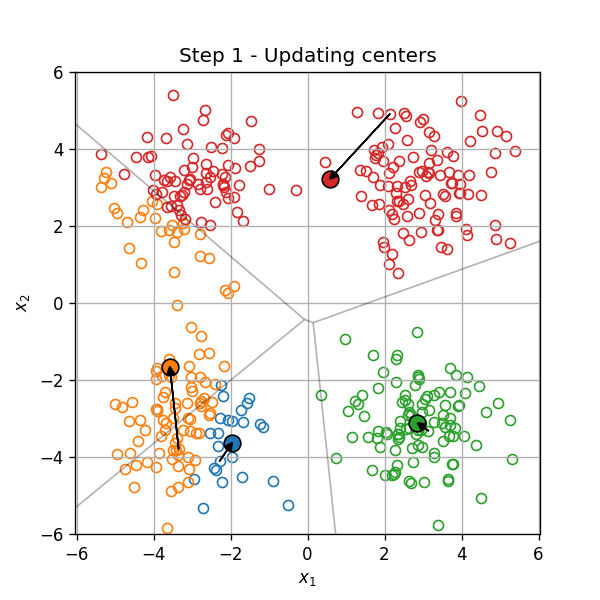
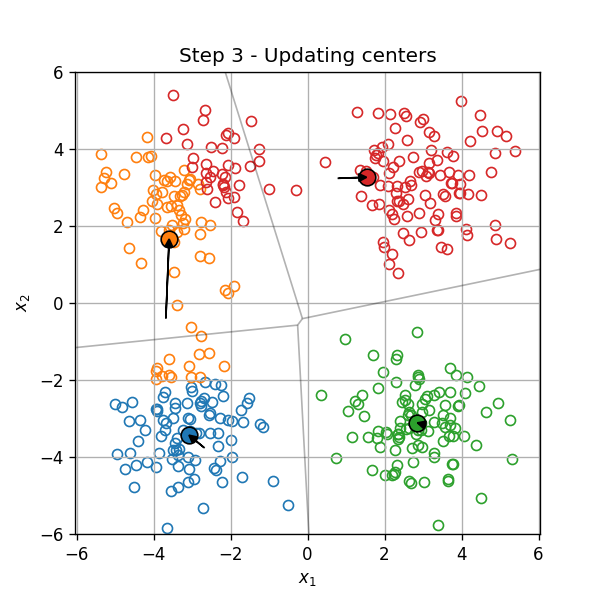
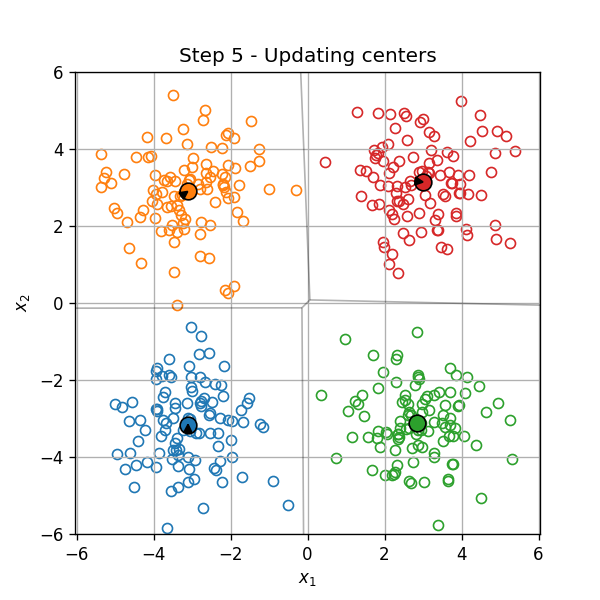
דוגמא

איתחול
חזרה עד להתכנסות:
- שיוך כל נקודה לאשכול, על פי המרכז הקרוב
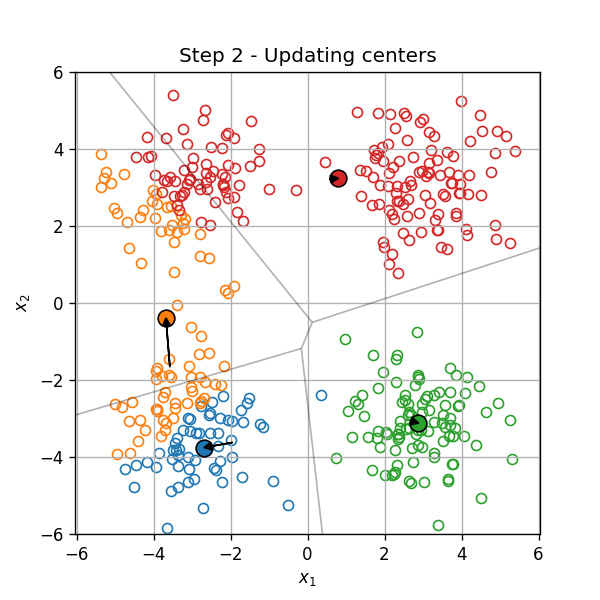
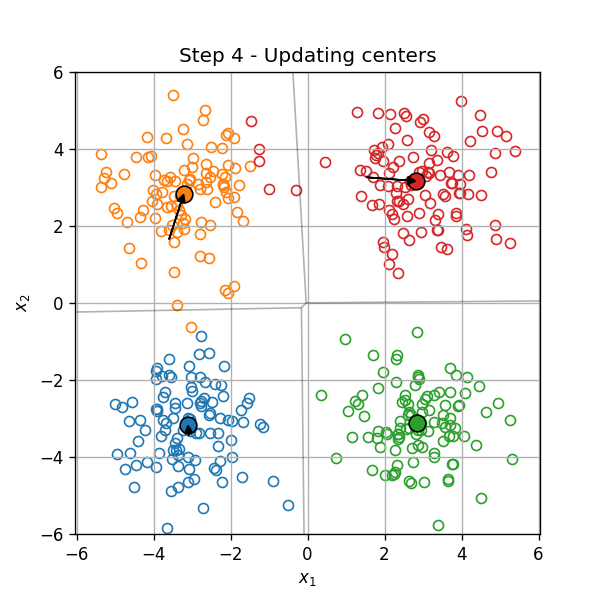
- עדכון מרכזי האשכולות

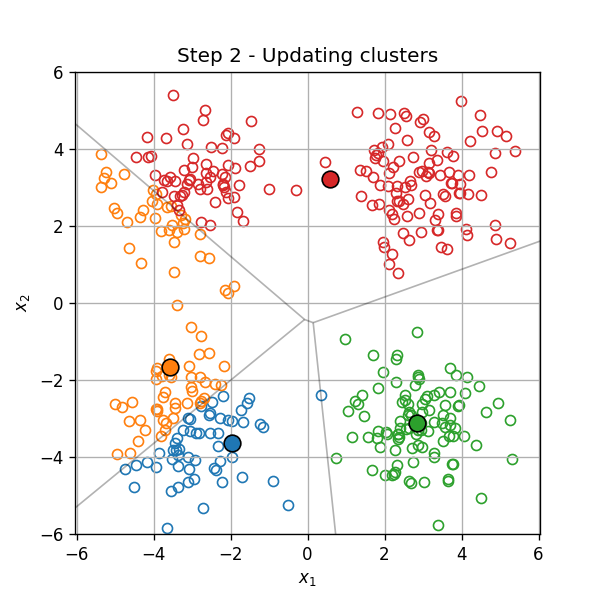
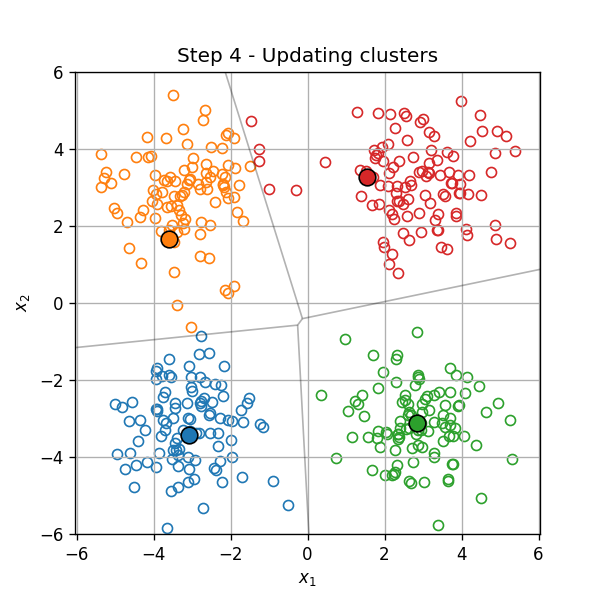
normal

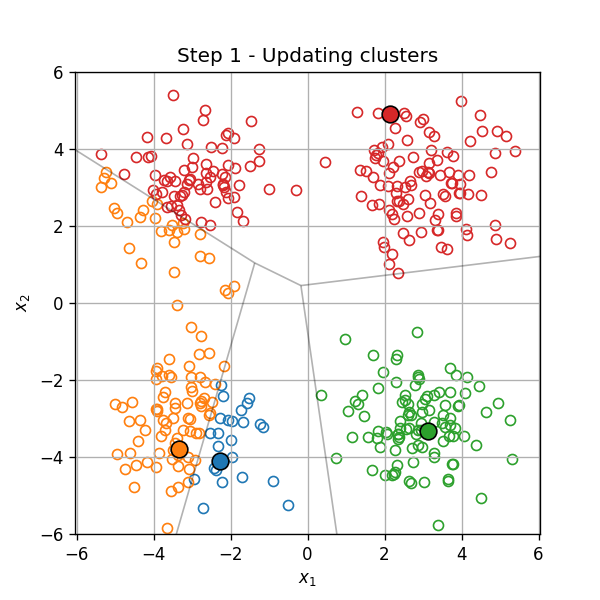
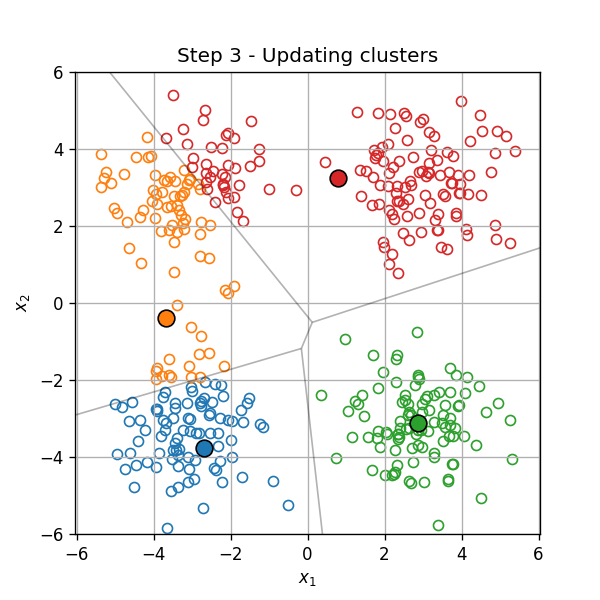
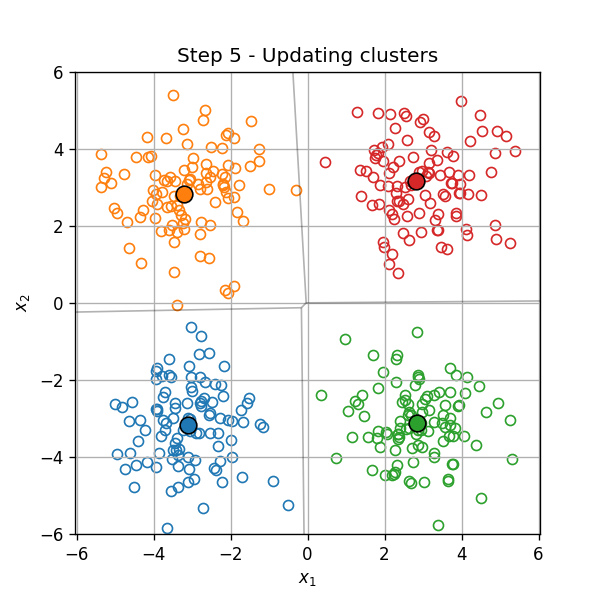
תכונות

מובטח כי פונקציית המטרה תקטן בכל צעד (אלגוריתם חמדן Greedy).
מובטח כי האלגוריתם יתכנס. זאת אומרת שהוא יעצר לאחר מספר סופי של עדכונים.
לא מובטח כי האלגוריתם יתכנס לפתרון האופטימאלי.
אתחולים שונים יכולים להוביל לתוצאות שונות.

בחירת מספר האשכולות K

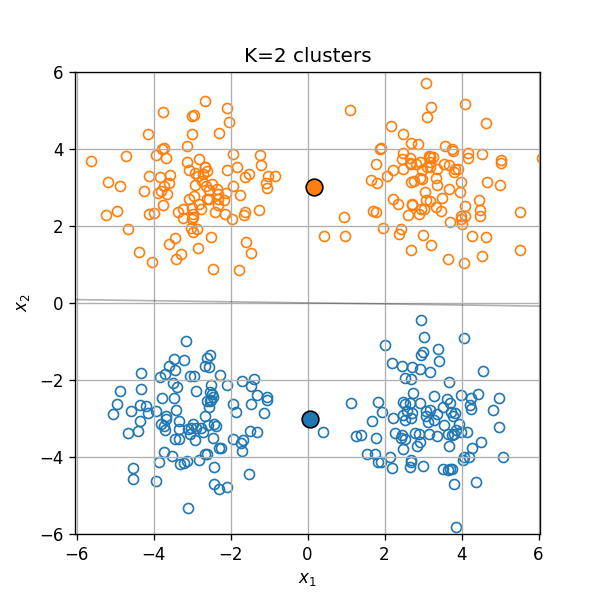
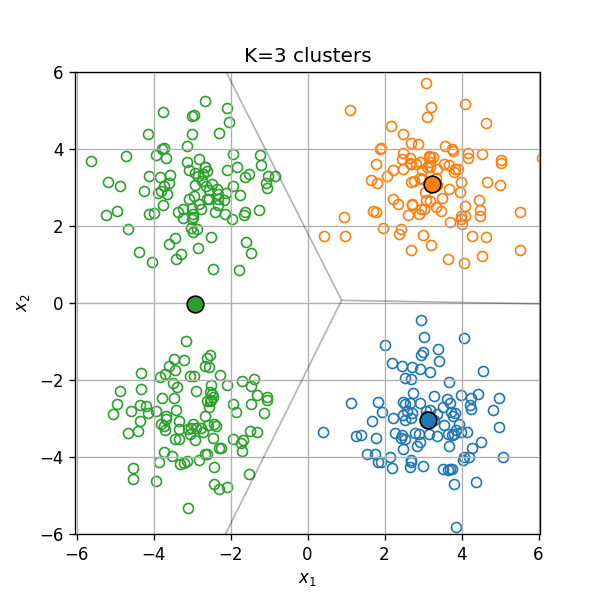
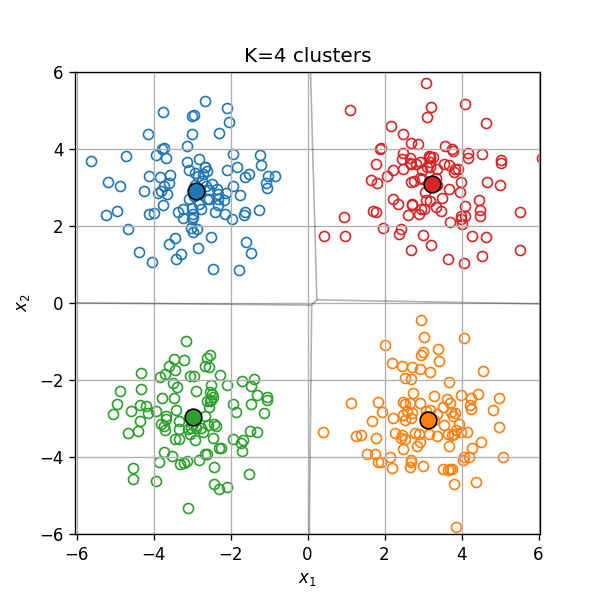
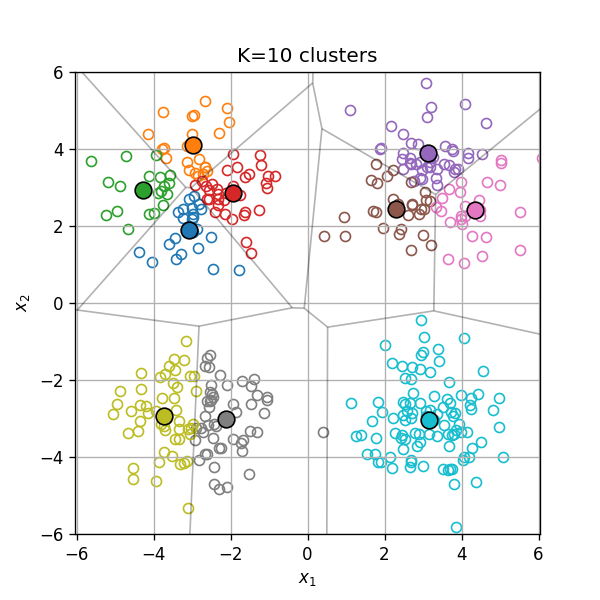
normal normal normal normal

במקרים מסויימים יהיה עלינו לקבוע את מספר האשכולות כתלות בנתונים.

בחירת מספר האשכולות K

שיטה לקביעת מספר האשכולות: שיפור יחסי קטן

שגיאת האשכול: שורש ממוצע הריבועים (Root Mean Square (RMS)) של המרחקים מהממוצעים:

$E\left(K\right)=\sqrt{\frac{1}{N}\sum_{i=1}^K\sum_{j\in G_i}\left\lVert \boldsymbol{x}_j-\boldsymbol{\mu}_i \right\rVert^2}$

מציאת הנקודה שבה הגדלת מספר האשכולות יתן שיפור היחסי זניח בשגיאת האשכול:

$\underset{K}{\arg\min}\quad K,\qquad\text{s.t.} \frac{E\left(K\right)-E\left(K+1\right)}{E\left(K\right)}\triangleq\frac{-\Delta E\left(K\right)}{E\left(K\right)}<\epsilon$

בחירת מספר האשכולות K

שיטה לקביעת מספר האשכולות: שיפור יחסי קטן - המשך

עבור הדוגמא ממקודם. גרף השגיאה:

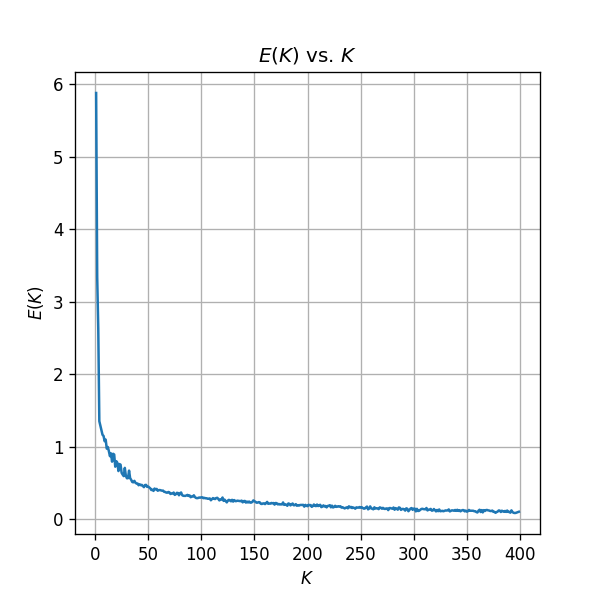
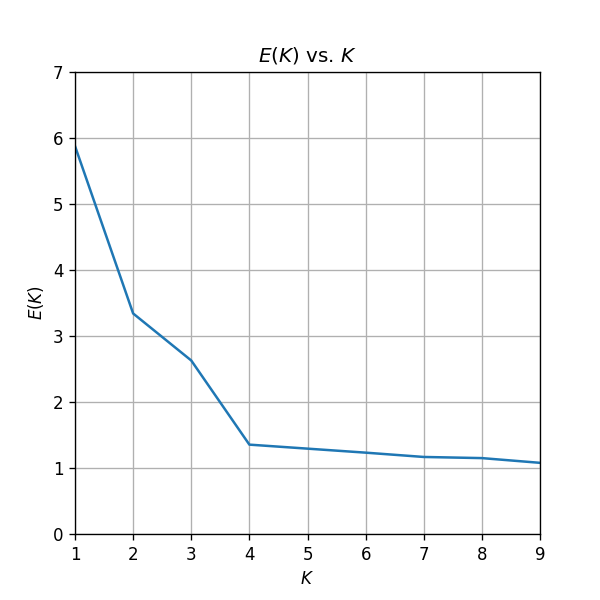
normal normal

בחירת מספר האשכולות K

שיטה לקביעת מספר האשכולות: שיפור יחסי קטן - המשך

גרף השיפור היחסי:

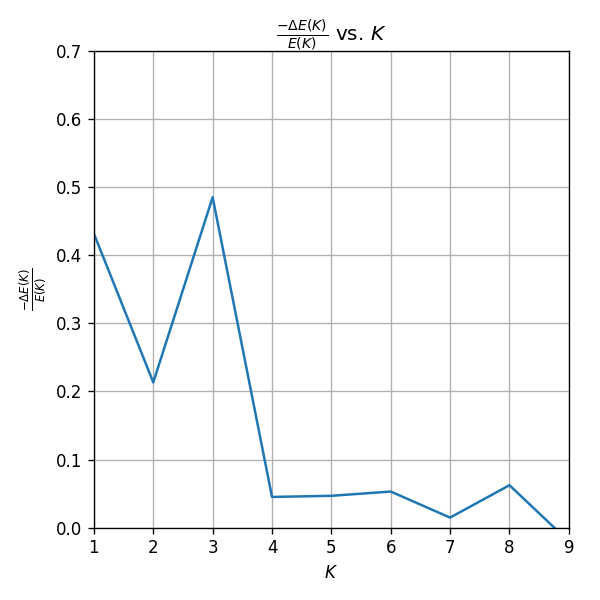
normal

בנקודה $K=4$ השיפור היחסי צונח משמעותית. לכן הגיוני לבחור 4 אשכולות.

תרגילים

✍️ תרגיל 4.1

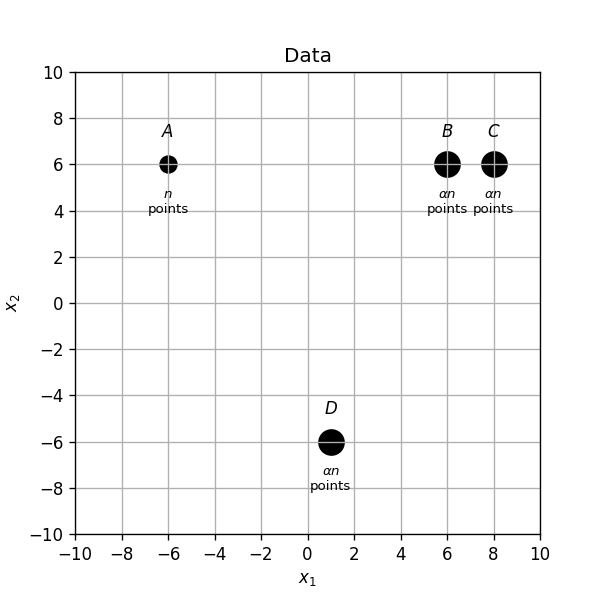
נתונות $\left(1+3\alpha\right)n$ נקודות שונות:

$n$ נקודות בקואורדינאטות $A=\left(-6,6\right)$
$\alpha n$ נקודות בכל אחת מהקואורדינאטות $B=\left(6,6\right),C=\left(8,6\right),D=\left(1,-6\right)$

א) מתאחלים את המרכזים על ידי בחירה אקראית של 3 מתוך ארבעת הנקודות A,B,C,D. לאילו חלוקות יתכנס האלגוריתם בעבור כל אחת מארבעת האתחולים האפשריים.

normal

💡 תרגיל 4.1א - פיתרון

א) נחשב את תוצאת האלגוריתם בעבור כל אחת מארבעת האתחולים:

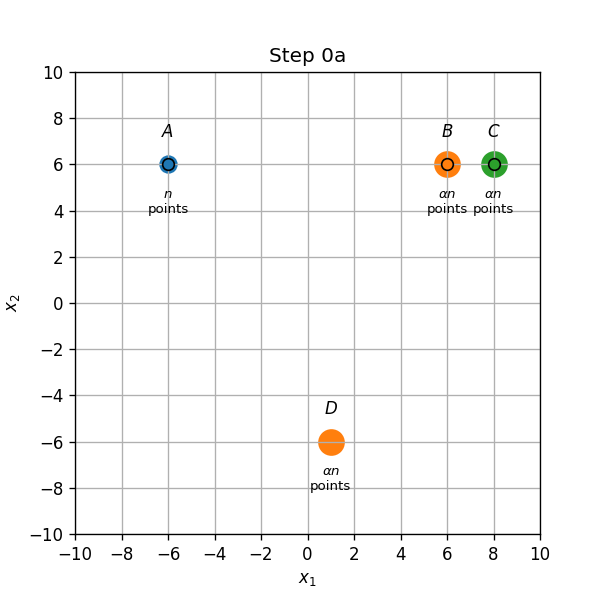
מרכזים ב A,B ו C:

שויך התחלתי (0a): נקודות בA,B ו C ישוייכו למרכז אשר הנמצא עליהם, והנקודות בD ישוייכו למרכז שבB.
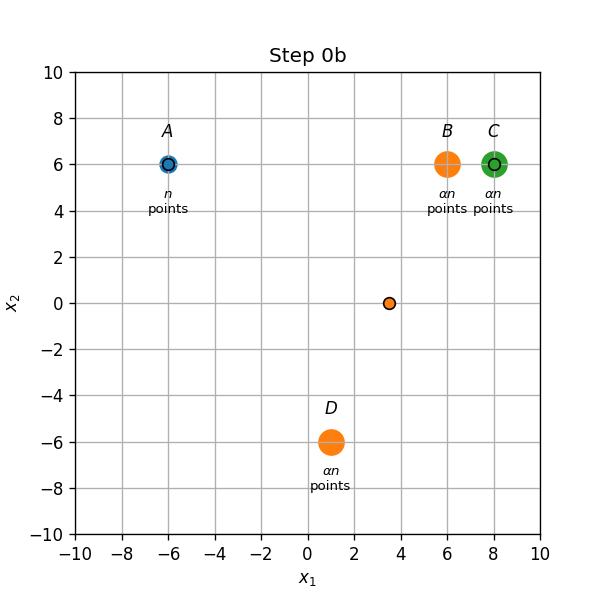
עדכון מרכזים (0b): המרכז שב B יזוז לאמצע הדרך שבין הנקודות B ו D.
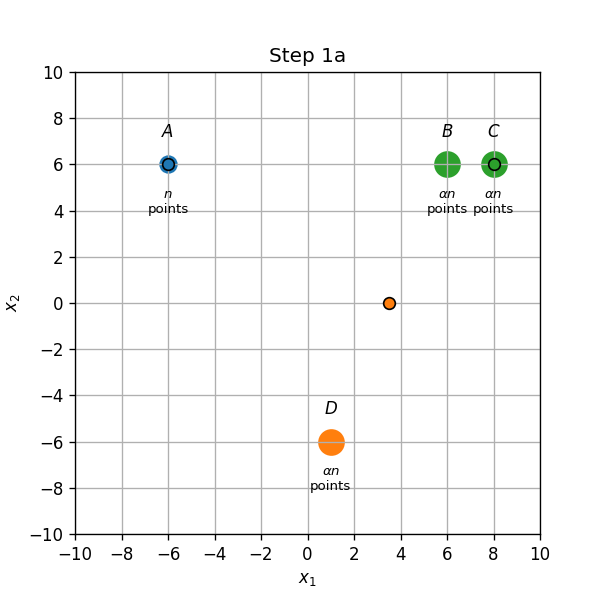
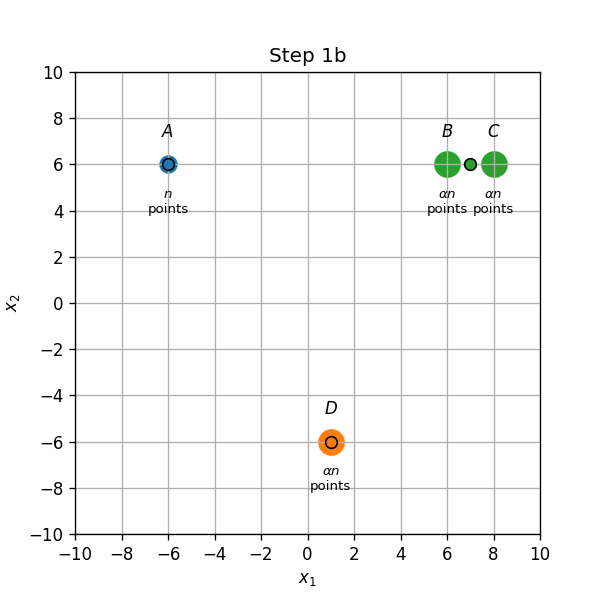
עדכון אשכולות (1a): הנקודת שבB ישוייכו כעת למרכז שבC.
עדכון מרכזים (1b): המרכז שבין B ל D יזוז לD, והמרכז שבC יזוז למחצית הדרך שבין B לC.

normal

💡 תרגיל 4.1א - פיתרון

מרכזים ב A,B ו D:

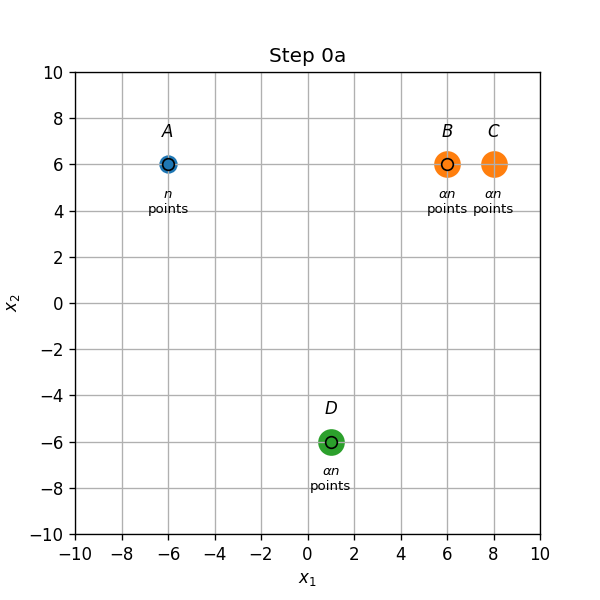
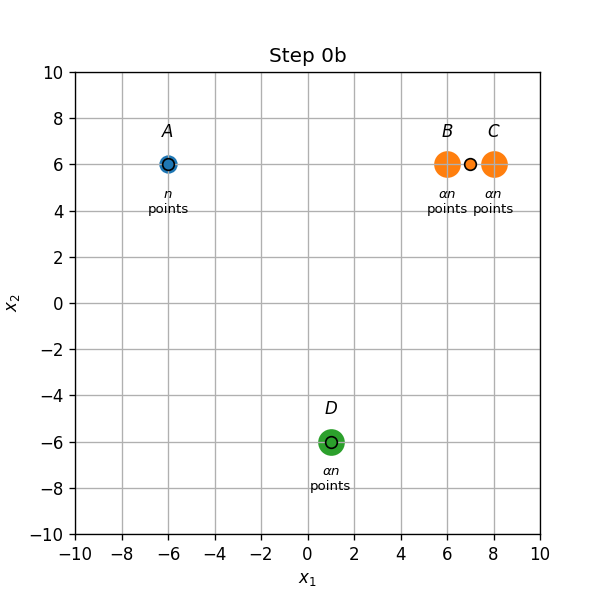
שויך התחלתי (0a): נקודות בA,B ו D ישוייכו למרכז אשר נמצא עליהם, והנקודות בC ישוייכו למרכז שבB.
עדכון מרכזים (0b): המרכז שב B יזוז לאמצע הדרך שבין הנקודות B ו C.

normal

💡 תרגיל 4.1א - פיתרון

מרכזים ב A,C ו D:

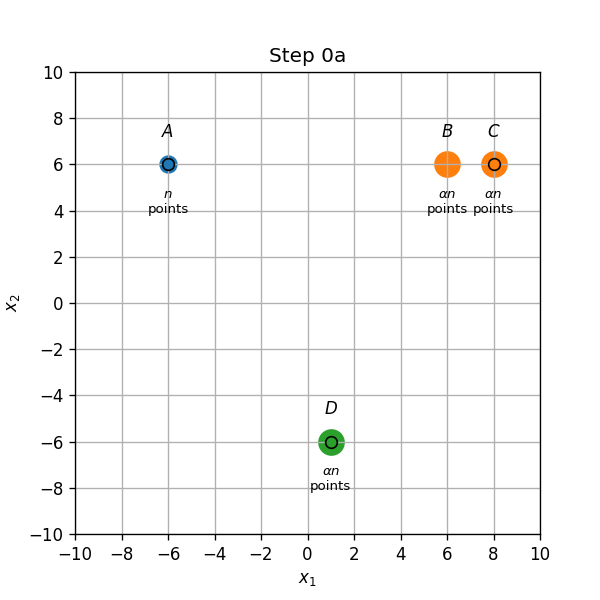
שויך התחלתי (0a): נקודות בA,C ו D ישוייכו למרכז אשר נמצא עליהם, והנקודות בB ישוייכו למרכז שבC.
עדכון מרכזים (0b): המרכז שב C יזוז לאמצע הדרך שבין הנקודות B ו C.

normal

💡 תרגיל 4.1א - פיתרון

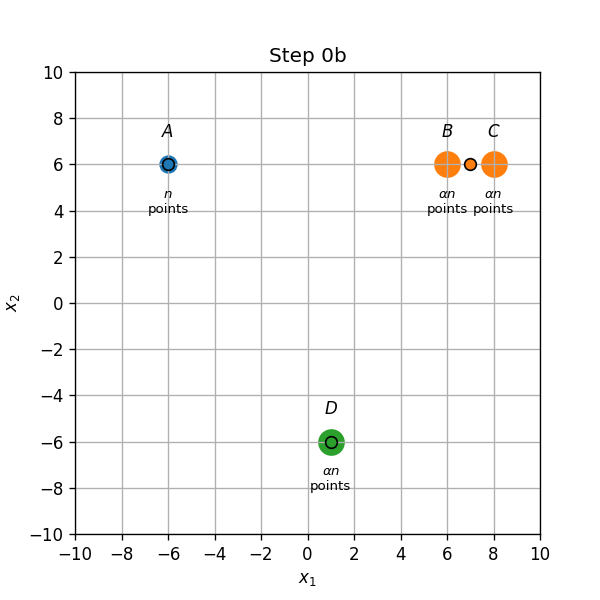
מרכזים ב B,C ו D:

שויך התחלתי (0a): נקודות בB,C ו D ישוייכו למרכז אשר נמצא עליהם, והנקודות בA ישוייכו למרכז שבB.
עדכון מרכזים (0b): המרכז שב B יזוז לנקודה שהיא המרכז של הנקודות A ו B. (משום שכמות הנקודות בשתי הקבוצות שונה, נקודה זו היא לא אמצע הדרך בניהם).

השלב הבא של עידכון האשכולות תלוי במיקום של המרכז החדש.

normal

normal normal

💡 תרגיל 4.1א - פיתרון

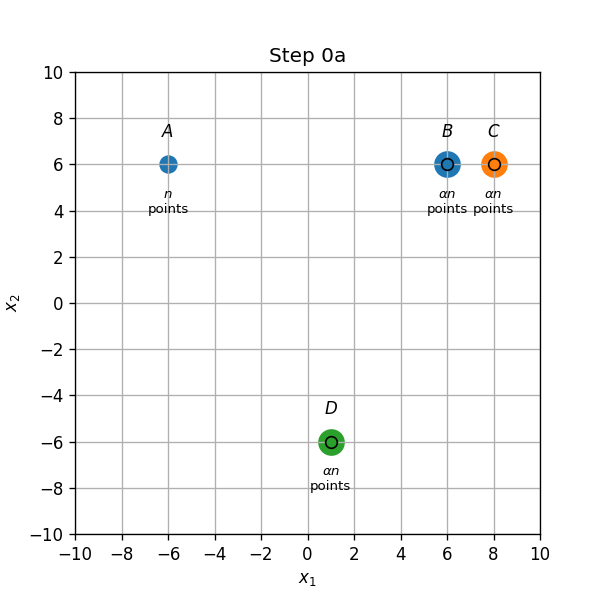
מרכזים ב B,C ו D:

מקרה 1:

המרכז החדש קרוב יותר לנקודה B משאר הנקודה C. והאלגוריתם הסתיים:

normal

💡 תרגיל 4.1א - פיתרון

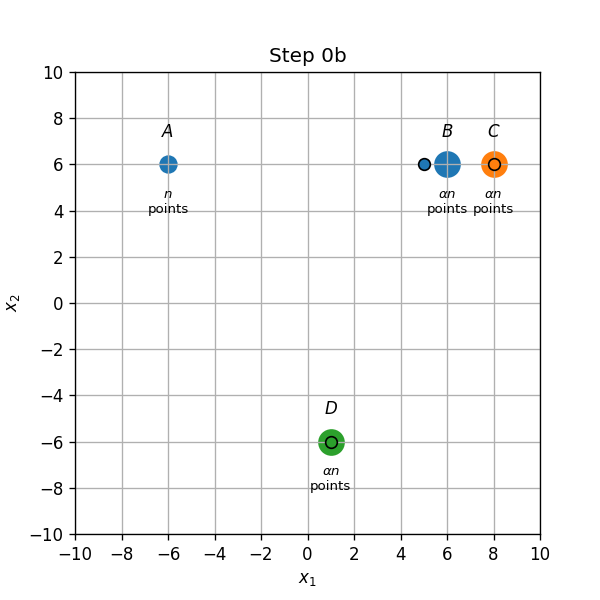
מרכזים ב B,C ו D:

מקרה 2:

המרכז החדש רחוק יותר לנקודה B משאר הנקודה C. אזי המשך יהיה:

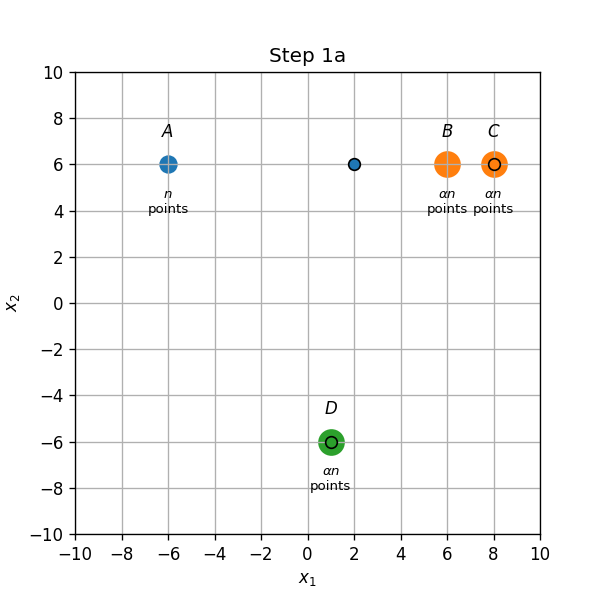
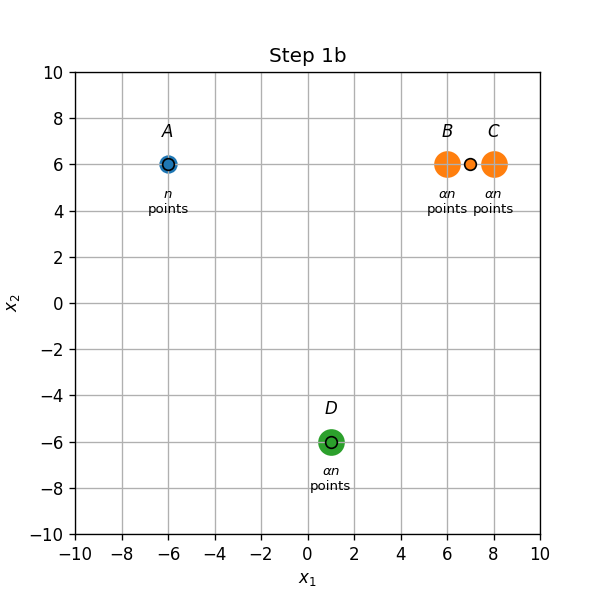
normal

💡 תרגיל 4.1א - פיתרון

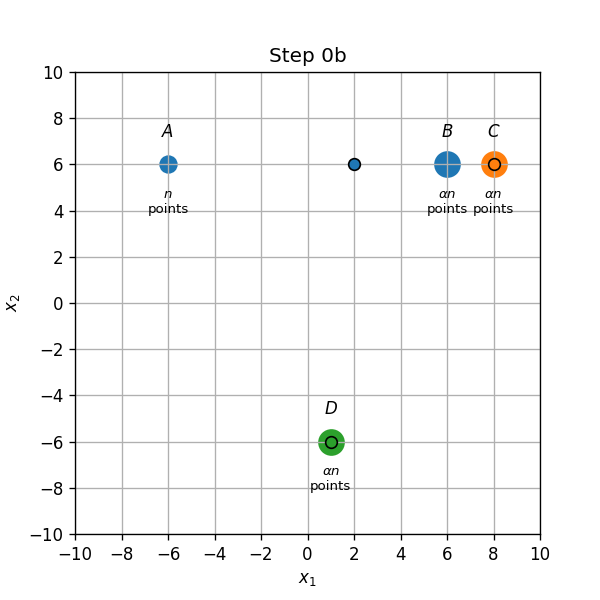
מרכזים ב B,C ו D:

מקרה 2:

נמצא את התנאי על $\alpha$ שבעבורו מתרחש מקרה 2.

נסמן ב $\boldsymbol{\mu}_1$ את המרכז שבין A לB:

$\boldsymbol{\mu}_1=\frac{n\vec{A}+\alpha n\vec{B}}{\left(1+\alpha\right)n}=\frac{\left(-6\hat{x}_1 + 6\hat{x}_2\right)+\alpha\left(6\hat{x}_1 + 6\hat{x}_2\right)}{1+\alpha}=\frac{\alpha-1}{\alpha+1}6\hat{x}_1 + 6\hat{x}_2$

על מנת שיתרחש עידכון על המרחק בין המרכז החדש נקודה B גדול מ2:

$\left\lVert\left(6\hat{x}_1 + 6\hat{x}_2\right)-\left(\frac{\alpha-1}{\alpha+1}6\hat{x}_1 + 6\hat{x}_2\right)\right\rVert>2 \\ \Leftrightarrow\alpha<5$

✍️ תרגיל 4.1

ב) מהו האשכול האופטימאלי (הממזער של פונקציית המטרה)? רשמו את הפתרון כתלות בפרמטר $\alpha$ . (ניתן להניח כי בפתרון האופטימאלי כל הנקודות שנמצאות באותו המקום משוייכות לאותו האשכול)

normal

💡 תרגיל 4.1ב - פיתרון

נרצה למזער את:

$\sum_{i=1}^K\frac{1}{2\left\lvert G_i\right\rvert}\sum_{j,k\in S_i}\left\lVert \boldsymbol{x}_j-\boldsymbol{x}_k \right\rVert^2$

נפסול פתרונות עם אשכול ריק. לכן הפתרון יהיה אחד מ:

(A,B), (C), (D)
(A,C), (B), (D)
(A,D), (B), (C)
(B,C), (A), (D)
(B,D), (A), (C)
(C,D), (A), (B)

💡 תרגיל 4.1ב - פיתרון - המשך

התרומה של האכולות עם נקודה בודדת הינה 0, ולכן יש לחשב רק את התרומה של האשכול שמכיל זוג נקודות. למשל בעבור (A,B), (C), (D):

$\sum_{i=1}^K\frac{1}{2\left\lvert G_i\right\rvert}\sum_{j,k\in S_i}\left\lVert \boldsymbol{x}_j-\boldsymbol{x}_k \right\rVert^2 =\frac{1}{N_A+N_B}\left(N_A N_B\left\lVert\vec{B}-\vec{A}\right\rVert^2\right)$

בעבור כל שאר האשכולות:

Clusters	Objective
(A,B), (C), (D)	$\frac{\alpha n^2}{\left(\alpha+1\right)n}12^2=144\frac{\alpha n}{\alpha+1}$
(A,C), (B), (D)	$\frac{\alpha n^2}{\left(\alpha+1\right)n}\left(7^2+12^2\right)=193\frac{\alpha n}{\alpha+1}$
(A,D), (B), (C)	$\frac{\alpha n^2}{\left(\alpha+1\right)n}14^2=196\frac{\alpha n}{\alpha+1}$
(B,C), (A), (D)	$\frac{\alpha^2 n^2}{2\alpha n}2^2=2\alpha n$
(B,D), (A), (C)	$\frac{\alpha^2 n^2}{2\alpha n}\left(5^2+6^2\right)=30.5\alpha n$
(C,D), (A), (B)	$\frac{\alpha^2 n^2}{2\alpha n}\left(7^2+6^2\right)=42.5\alpha n$

לכן הפתרון יהיה (A,B),(C),(D) או (B,C),(A),(D)

💡 תרגיל 4.1ב - פיתרון - המשך

נבדוק בעבור אלו ערכים של $\alpha$ האשכול הראשון הינו האופטימאלי (ולהפיך):

$144\frac{\alpha n}{\alpha+1}<2\alpha n \\ \Leftrightarrow \alpha>71$

בעבור $\alpha>71$ הפתרון האופטימאלי הינו (A,B),(C),(D).
בעבור $\alpha<71$ הפתרון האופטימאלי הינו (B,C),(A),(D).

עבור התוצאות מהסעיף הקודם:

בעבור $\alpha>71$ הפתרון האופטימאלי הינו (A,B),(C),(D), אך עבור 3 מתוך 4 האיחולים שבדקנו האלגוריתם התכנס לפתרון של (B,C),(A),(D).
בעבור $\alpha<71$ הפתרון האופטימאלי הינו (B,C),(A),(D), אך במקרה של $\alpha>5$ ואתחול של מרכזים ב B,C ו D מתקבל הפתרון של (A,B),(C),(D).

✍️ תרגיל 4.1

ג) האם קיים אתחול אשר בעבורו האלגוריתם לא יתכנס לפתרון בעל הערך המינימאלי שמצאתם בסעיף הקודם? הדגימו.

normal

פיתרון

כל מקרים שצויינו בסעיף הקודם. בנוסף,ניתן לדוגמא לאתחל שניים מתוך שלושת המרכזים בנקודות מאד רחוקות, ואז כל הנקודות ישוייכו למרכז השלישי.

בעיה מעשית

🚖 תזכורת: מדגם נסיעות המונית בNew York

עשרת הדגמים הראשונים במדגם הנסיעות בעיר New York

	passenger_count	trip_distance	payment_type	fare_amount	tip_amount	pickup_easting	pickup_northing	dropoff_easting	dropoff_northing	duration	day_of_week	day_of_month	time_of_day
0	2	2.768065	2	9.5	0.00	586.996941	4512.979705	588.155118	4515.180889	11.516667	3	13	12.801944
1	1	3.218680	2	10.0	0.00	587.151523	4512.923924	584.850489	4512.632082	12.666667	6	16	20.961389
2	1	2.574944	1	7.0	2.49	587.005357	4513.359700	585.434188	4513.174964	5.516667	0	31	20.412778
3	1	0.965604	1	7.5	1.65	586.648975	4511.729212	586.671530	4512.554065	9.883333	1	25	13.031389
4	1	2.462290	1	7.5	1.66	586.967178	4511.894301	585.262474	4511.755477	8.683333	2	5	7.703333
5	5	1.561060	1	7.5	2.20	585.926415	4512.880385	585.168973	4511.540103	9.433333	3	20	20.667222
6	1	2.574944	1	8.0	1.00	586.731409	4515.084445	588.710175	4514.209184	7.950000	5	8	23.841944
7	1	0.804670	2	5.0	0.00	585.344614	4509.712541	585.843967	4509.545089	4.950000	5	29	15.831389
8	1	3.653202	1	10.0	1.10	585.422062	4509.477536	583.671081	4507.735573	11.066667	5	8	2.098333
9	6	1.625433	1	5.5	1.36	587.875433	4514.931073	587.701248	4513.709691	4.216667	3	13	21.783056

❓️ הבעיה: מציאת חניונים

חברת מוניות רוצה לשכור $K$ מגרשי חניה ברחבי העיר NYC בהם יוכלו לחכות המוניות שלה בין הנסיעות.

לשם כך היא מעוניינת לבחור באופן אופטימאלי את המיקומים של מגרשי החניות האלו כך שהמרחק הממוצע מנקודת הורדת הנוסע למרגש החניה הקרוב יהיה מינימאלי.

שדות רלוונטיים

הפעם נתמקד בשתי השדות:

dropoff_easting - הקואורדינאטה האורכית (מזרח-מערב) של סיום הנסיעה
dropoff_northing - הקואורדינאטה הרוחבית (צפון-דרום) של סיום הנסיעה

(למתעניינים: הקואורדינאטות נתונות בUTM-WGS84, היחידות הן בקירוב קילומטר).

❓️ הבעיה: מציאת חניונים - משך

ויזואליזציה של נקודות ההורדה

png

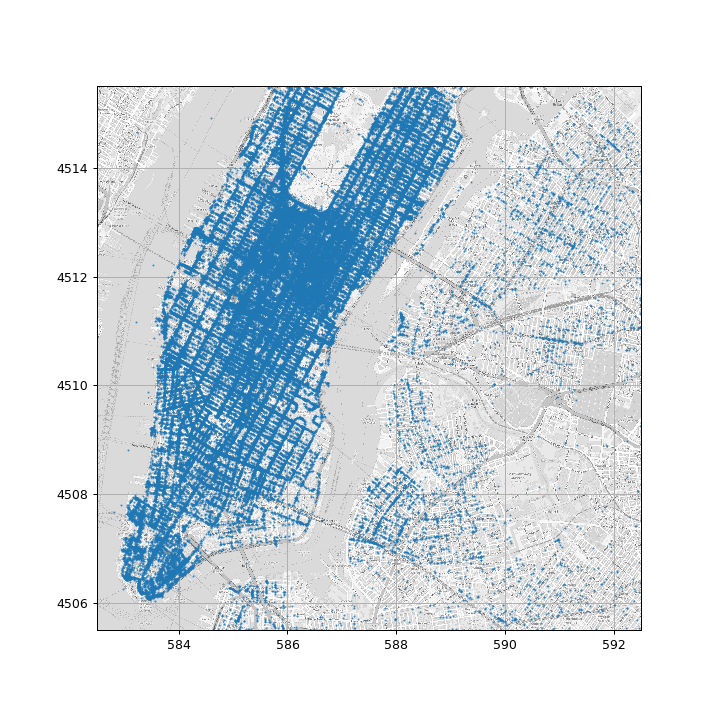
הגדרה פורמאלית של הבעיה

נשתמש בסימונים הבאים:

$X$ הוקטור האקראי של מיקום סיום הנסיעה
$\boldsymbol{c}_i$ : המיקום של החניות ה- $i$ .
$N$ : מספר הנסיעות במדגם.

המטרה: למצוא את מיקומי החניונים האופטימאליים אשר ממזערים את:

$R\left(\left\lbrace\boldsymbol{c}_i\right\rbrace\right)=\mathbb{E}\left[\min_{i}\left\lVert\boldsymbol{x}-\boldsymbol{c}_i\right\rVert\right]$

מכיוון שאנו לא יודעים משהו הפילוג של $X$ נחליף את התחולת על $X$ בתוחלת האימפירית

$\hat{R}\left(\left\lbrace\boldsymbol{c}_i\right\rbrace\right)=\frac{1}{N}\sum_{j}\min_{i}\left\lVert\boldsymbol{x}_j-\boldsymbol{c}_i\right\rVert$

הגדרה פורמאלית של הבעיה - המשך

$\hat{R}\left(\left\lbrace\boldsymbol{c}_i\right\rbrace\right)=\frac{1}{N}\sum_{j}\min_{i}\left\lVert\boldsymbol{x}_j-\boldsymbol{c}_i\right\rVert$

את הבעיה שקיבלנו ניתן לרשום כבעיית אשכול. נגדיר את האשכול $G_i$ , כאוסף כל הנסיעות שהחניון ה $i$ הוא הקרוב ביותר.

$\hat{R}\left(\left\lbrace\boldsymbol{c}_i\right\rbrace\right)=\frac{1}{N}\sum_{i=1}^K\sum_{j\in G_i}\left\lVert\boldsymbol{x}_j-\boldsymbol{c}_i\right\rVert$

פתרון באמצעות K-Means

$\hat{R}\left(\left\lbrace\boldsymbol{c}_i\right\rbrace\right)=\frac{1}{N}\sum_{i=1}^K\sum_{j\in G_i}\left\lVert\boldsymbol{x}_j-\boldsymbol{c}_i\right\rVert$

הבעיה שקיבלנו דומה מאד לK-Means, אם הבדל משמעותי אחד.
K-Means ממזער את המרחק הריבועי הממוצע בעוד שאנו מחפשים למזער את המרחק האוקלידי.

זהו מצב נפוץ שבו איננו מסוגלים לפתור בעיה מסויימת באופן ישיר אז אנו פותרים בעיה דומה לה, בתקווה לקבל תוצאות מספקות.

הרצה

png

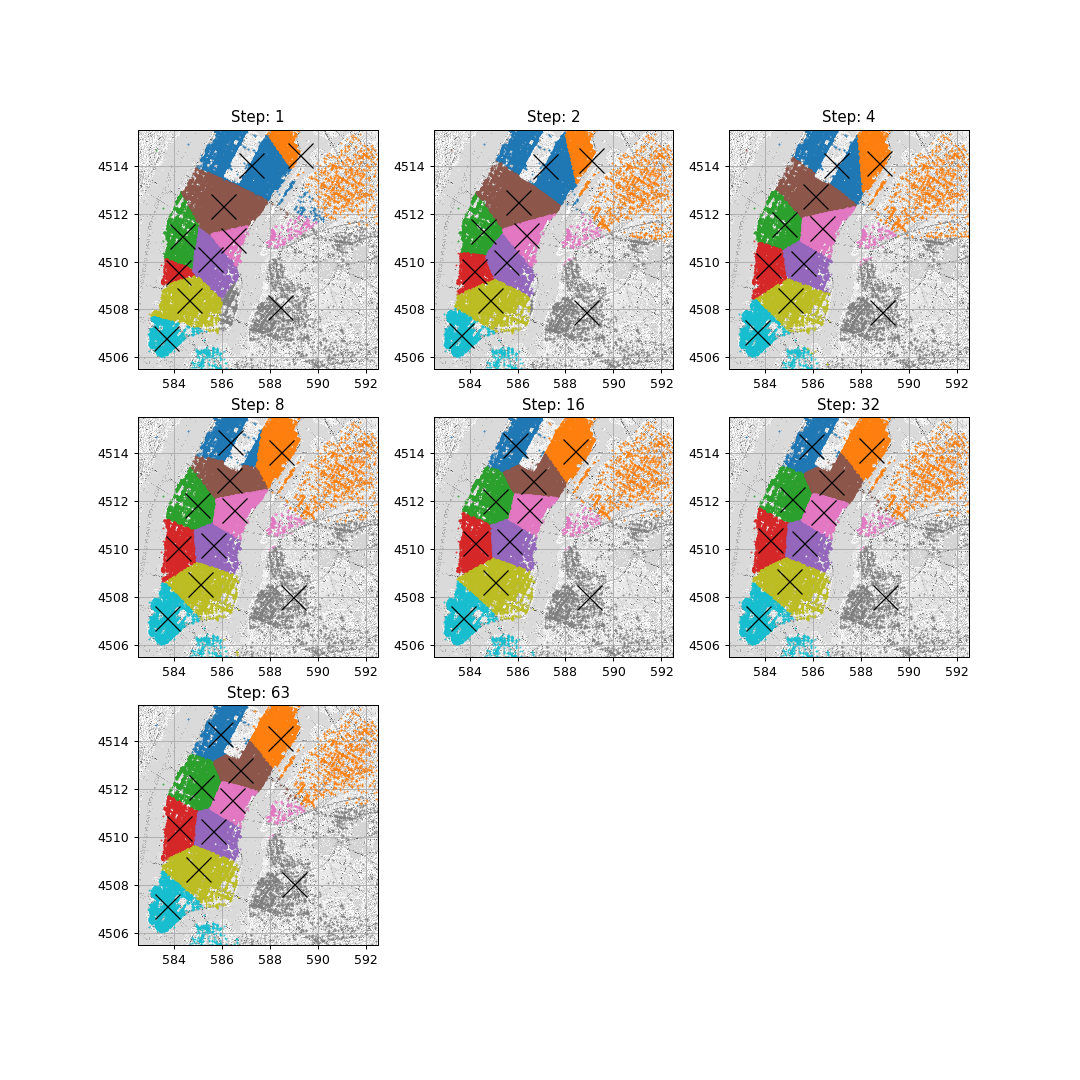
המרחק נסיעה הממוצע המתקבל הינו 700 מ’.

✍️ תרגיל 4.2

1) ציינו שתי סיבות מדוע המיקומים שקיבלנו הם לא בהכרח אופטימאליים

2) הציעו דרכים לשפר את התוצאות על סמך הסיבות מסעיף הקודם.

פתרון

1) K-Mean לא מבטיח התכנסות למינימום הגולבאלי. ניתן להריץ את האלגוריתם מספר פעמים עם איתחולים שונים.

2) K-Mean ממזערת את השגיאה הריבועית הממוצעת. ניתן לשפר על ידי תיקון המרכז לנקודה אשר ממזערת את המרחק עצמו.

הערה: ראו חציון הגיאומטרי The Geometric Median (wiki) ו Weiszfeld’s algorithm.

❓️ בעיה 2: מציאת מספר החניונים האופטימאלי

עד כה השתמשנו ב10 חניונים.
נרצה כעת לבחור גם מספר זה בצורה מיטבית

נניח כי:

עלות האחזקה של חניון הינה 10k$ לחודש.
בכל חודש יהיו בדיוק 100k נסיעות.
עלות הנסיעה של מונית בדרך לחניון הינה 3$ לקילומטר.

נרשום תחת הנחות אלו את העלות החודשית של אחזקת החניונים והנסיעה אליהם:

$R\left(\left\lbrace\boldsymbol{c}_i\right\rbrace, K\right)= 10\cdot K+100\cdot3\cdot\mathbb{E}\left[\min_{j}\left\lVert\boldsymbol{x}-\boldsymbol{c}_j\right\rVert\right]$

והמקבילה האמפירית:

$\hat{R}\left(\left\lbrace\boldsymbol{c}_i\right\rbrace, K\right)= 10\cdot K+300\cdot\frac{1}{N}\sum_{i=1}^K\sum_{\boldsymbol{x}_j\in G_i}\left\lVert\boldsymbol{x}_j-\boldsymbol{c}_i\right\rVert$

מספר החניונים כHyper parameter

כעת עלינו לבצע אופטימיזציה גם על מספר החניונים וגם המיקום שלהם.
ראינו כיצד ניתן למצוא פתרון בעבור $K$ נתון.
חל נעבור על כל ערכי $K$ הרלוונטים, וניקח הפתרון הטוב ביותר.

פרמטרים שאין לנו שיטה יעילה לבחור אותם אנו מכנים לרוב הHyper-parameters של המודל.
שני hyper-parameters בהם כבר נתקלנו בקורס הינם:
- מספר ורוחב התאים של היסטוגרמה
- רוחב וסוג הגרעין בKDE

לרוב נאלץ לבחור את ערכם של הhyper-parameters על ידי:

חיפוש על גריד (grid search) או מעבר על כל האפשרויות (brute force).
ניסוי וטעיה. כאשר לרוב נתחיל מאיזשהו ניחוש מושכל.

פתרון באמצעות K-Means וסריקת על K.

נריץ את אלגוריתם הK-Means בעבור כל ערך של $K$ בתחום $1\leq K \leq 25$ :

png

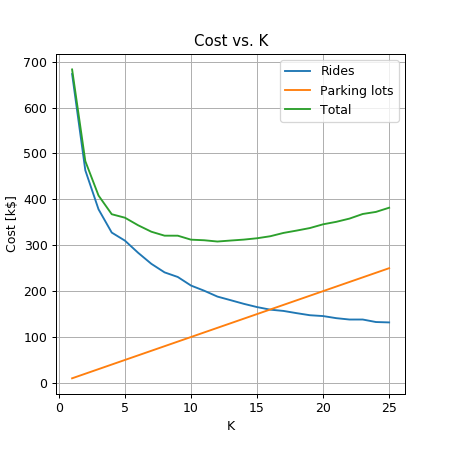
נקבל כי:

מספר החניונים האופטימאלי הינו: 12.
מרחק הנסיעה הממוצע יהיה 630 מ’.
העלות הכוללת תהיה 308.12k$ לחודש.

תרגילים נוספים

✍️ תרגיל 4.3

נתבונן בבעיית “האשכול” החד-מימדית הבאה: normal

כאשר הנקודות $\left\lbrace x_i\right\rbrace_{i=0}^N$ ממוקמות באופן אחיד באינטרוול $\left[0,d\right]$ ומספרן $N\rightarrow\infty$ . (וכמובן $\Delta\rightarrow 0$ ).

הראו כי האלגוריתם K-Means עם $K=2$ מתכנס למינימום הגלובלי של השגיאה הריבועית מכל תנאי התחלה סביר (כלומר, המרכזים ההתחלתיים ממוקמים באינטרוול $\left[0,d\right]$ ).

💡 פיתרון

נסמן ב $x^{\left(t\right)}$ את נקודת ההחלטה באיטרציה $t$
וב- $\mu_2^{\left(t\right)},\mu_1^{\left(t\right)}$ את המרכזים באיטרציה $t$

בצעד הראשון נקבל כי:

$x^{\left(0\right)}=\frac{\mu_1^{\left(0\right)}+\mu_2^{\left(0\right)}}{2}$

באיטרציה ה $t$ נקבל ש:

$\begin{cases} \mu_1^{\left(t\right)}=\frac{1}{2} x^{\left(t-1\right)}\\ \mu_2^{\left(t\right)}=\frac{x^{\left(t-1\right)}+d}{2}\\ \end{cases}\\ \Rightarrow x^{\left(t\right)}=\frac{\mu_1^{\left(t\right)}+\mu_2^{\left(t\right)}}{2}=\frac{1}{2}x^{\left(t-1\right)}+\frac{1}{4}d$

💡 פיתרון - המשך

$x^{\left(t\right)}=\frac{\mu_1^{\left(t\right)}+\mu_2^{\left(t\right)}}{2}=\frac{1}{2}x^{\left(t-1\right)}+\frac{1}{4}d$

נרשום את כלל הרקוסרסיה של $x^{\left(t\right)}$ :

$\begin{aligned} x^{\left(t\right)} & = \frac{1}{2}x^{\left(t-1\right)}+\frac{1}{4}d \\ & = \frac{1}{2}\left(\frac{1}{2}x^{\left(t-2\right)}+\frac{1}{4}d\right)+\frac{1}{4}d \\ & = \frac{1}{2}\left(\frac{1}{2}\left(\frac{1}{2}x^{\left(t-3\right)}+\frac{1}{4}d\right)+\frac{1}{4}d\right)+\frac{1}{4}d \\ & = \frac{1}{2^t}x^{\left(0\right)}+\frac{d}{4}\sum_{i=0}^{t-1}\frac{1}{2^i} \end{aligned}$

מכאן שבגבול $t\rightarrow\infty$ מתקיים כי $x^{\left(t\right)}\rightarrow\frac{d}{2}$ , שזהו כמובן הפתרון האופטימאלי (חלוקה של הקטע לשני חלקים שווים).

תרגול 4K-Means

תיאוריה -אשכול

המטרה

דוגמאות

אלגוריתמי אשכול שונים

האלגוריתם K-means

האלגוריתם K-means

הבעיה השקולה

האלגוריתם K-means

שלבי האלגוריתם

דוגמא

תכונות

בחירת מספר האשכולות K

בחירת מספר האשכולות K

שיטה לקביעת מספר האשכולות: שיפור יחסי קטן

בחירת מספר האשכולות K

שיטה לקביעת מספר האשכולות: שיפור יחסי קטן - המשך

בחירת מספר האשכולות K

שיטה לקביעת מספר האשכולות: שיפור יחסי קטן - המשך

תרגילים

✍️ תרגיל 4.1

💡 תרגיל 4.1א - פיתרון

💡 תרגיל 4.1א - פיתרון

💡 תרגיל 4.1א - פיתרון

💡 תרגיל 4.1א - פיתרון

💡 תרגיל 4.1א - פיתרון

💡 תרגיל 4.1א - פיתרון

💡 תרגיל 4.1א - פיתרון

✍️ תרגיל 4.1

💡 תרגיל 4.1ב - פיתרון

💡 תרגיל 4.1ב - פיתרון - המשך

💡 תרגיל 4.1ב - פיתרון - המשך

✍️ תרגיל 4.1

פיתרון

בעיה מעשית

🚖 תזכורת: מדגם נסיעות המונית בNew York

❓️ הבעיה: מציאת חניונים

שדות רלוונטיים

❓️ הבעיה: מציאת חניונים - משך

ויזואליזציה של נקודות ההורדה

הגדרה פורמאלית של הבעיה

הגדרה פורמאלית של הבעיה - המשך

פתרון באמצעות K-Means

הרצה

✍️ תרגיל 4.2

פתרון

❓️ בעיה 2: מציאת מספר החניונים האופטימאלי

מספר החניונים כHyper parameter

פתרון באמצעות K-Means וסריקת על K.

תרגילים נוספים

✍️ תרגיל 4.3

💡 פיתרון

💡 פיתרון - המשך

תרגול 4
K-Means