תרגול 3
שיערוך פילוג בשיטות פרמטריות

תיאוריה

המטרה

להעריך את $p\left(\boldsymbol{x}\right)$ מתוך $n$ הדוגמאות ב $D$ .

כפי שנלמד בהרצאה, ניתן להבחין בין הגישות הבאות להסקה סטטיסטית:

גישה פרמטרית לעומת גישה לא-פרמטרית (א-פרמטרית)

גישה בייסיאנית לעומת גישה לא-בייסיאנית (קלאסית \ תדירותית).

הגישה הפרמטרית והלא פרמטרית

הבעיה בגישה הלא פרמטרית

- מניחה כי יש מספיק של דגימות בכל איזור.
- הבעיה: גודל המדגם שאנו צריכים גדל אקספונציאלית עם מספר המשתנים.

התוצאה המתקבלת אינה פונקציה שנוח לעבוד איתה.

הגישה הפרמטרית

נציע משפחה של פונקציות פרמטריות (לדוגמא משפחת הגאוסיאנים)

נקווה כי נוכל לקרב את פונקציית הפילוג בעזרת אחת הפונקציות מהמשפחה

את משפחת הפונקציות הזו אנו מכנים המודל, או המודל הפרמטרי.

את סט הפרמטרים של המודל נייצג כוקטור ונסמנו ב $\boldsymbol{\theta}$ .

המטרה

בהינתן מודל פרמטרי + מדגם: לשערך את וקטור הפרמטרים האופטימאלי $\hat{\boldsymbol{\theta}}^*$ .

הגישה באייסיאנית והלא-בייסיאנית

הגישה באייסיאנית

מניחים כי וקטור הפרמטרים $\boldsymbol{\theta}$ הינו וקטור אקראי.

הפילוג $p\left(\boldsymbol{\theta}\right)$ :

נקרא הפילוג הפריורי (prior distribution) או הא-פריורי (a priori distribution)

הפילוג $p\left(\boldsymbol{\theta}\lvert D\right)$ :

נקרא הפילוג הפוסטריורי (posterior distribution) או א-פוסטריורי (a posteriori distribution) (או הפילוג בדיעבד).

נבחר לרוב את המשערך על פי ההסתברות המקסימאלית, התוחלת וכו’ של הפילוג הא-פוסטריורי.

הגישה באייסיאנית והלא-בייסיאנית

הגישה הלא-בייסיאנית (המכונה גם: קלאסית או תדירותית (Frequintist))

מניחים כי וקטור הפרמטרים הינו גודל קבוע, אך לא יודע.

אין כל העדפה של ערך מסויים של הוקטור על פני ערך אחר.

נסמן $p\left(D;\boldsymbol{\theta}\right)$ במקרה שהפילוג תלוי בפרמטרים.

נסמן את פונקציית הסבירות (likelihood):

$\mathcal{L}\left(\boldsymbol{\theta}\right)\triangleq p\left(D;\boldsymbol{\theta}\right)$

שיטות שיערוך

משערך (Maximum a Posteriori (MAP (שיטה בייסיאנית)

המשערך האופטימאלי: וקטור הפרמטרים אשר ממקסם את צפיפות ההסתברות האפוסטריורית

$\hat{\boldsymbol{\theta}}_{\text{MAP}}=\underset{\boldsymbol{\theta}}{\arg\max}\quad p\left(\boldsymbol{\theta}\lvert D\right)$

שיטות שיערוך

משערך (Maximum a Posteriori (MAP (שיטה בייסיאנית) - המשך

נשתמש לרוב בכלל בייס:

$\begin{aligned} \hat{\boldsymbol{\theta}}_{\text{MAP}} & = \underset{\boldsymbol{\theta}}{\arg\max}\quad p\left(\boldsymbol{\theta}\lvert D\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \frac{p\left(D\lvert\boldsymbol{\theta}\right)p\left(\boldsymbol{\theta}\right)}{p\left(D\right)} \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad p\left(D\lvert\boldsymbol{\theta}\right)p\left(\boldsymbol{\theta}\right) \end{aligned}$

אנו מחפשים את המקסימום של המכפלה של:

הסבירות: $p\left(D\lvert\hat{\boldsymbol{\theta}}\right)$
צפיפות ההסתברות הא-פריורית: $p\left(\boldsymbol\theta\right)$

שיטות שיערוך

משערך Maximum Likelihood Estimator (MLE) (שיטה לא בייסיאנית)

המשערך האופטימאלי: וקטור הפרמטרים אשר ממקסם את פונקציית הסבירות

הlog-likelihood והנחת הIID

תחת ההנחה כי הדגמים במדגם הינם IID:

$p\left(D;\boldsymbol{\theta}\right)=p\left(\left\lbrace \boldsymbol{x}_i\right\rbrace_{i=1}^N;\boldsymbol{\theta}\right)=\prod_{i=1}^N p\left(\boldsymbol{x}_i;\boldsymbol{\theta}\right)$

משום ש $\log$ הינה פונקציה מונוטונית עולה:

$\underset{x}{\arg\max}\quad f\left(x\right)=\underset{x}{\arg\max}\quad \log\left(f\left(x\right)\right)$

נסמן:

$l\left(\boldsymbol{\theta}\right)\triangleq \log\left(\mathcal{L}\left(\boldsymbol{\theta}\right)\right)$

הlog-likelihood והנחת הIID - המשך

מכאן ש:

$\begin{aligned} \hat{\boldsymbol{\theta}}_{\text{MLE}} & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \mathcal{L}\left(\boldsymbol{\theta}\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad l\left(\boldsymbol{\theta}\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \log\left(p\left(D;\boldsymbol{\theta}\right)\right)\\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \log\left(\prod_{i=1}^N p\left(\boldsymbol{x}_i;\boldsymbol{\theta}\right)\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \sum_{i=1}^N\log\left(p\left(\boldsymbol{x}_i;\boldsymbol{\theta}\right)\right) \end{aligned}$

הlog-likelihood והנחת הIID - המשך 2

באופן זהה:

$\begin{aligned} \hat{\boldsymbol{\theta}}_{\text{MAP}} & = \underset{\boldsymbol{\theta}}{\arg\max}\quad p\left(D\lvert\boldsymbol{\theta}\right)p\left(\boldsymbol{\theta}\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \sum_{i=1}^N\log\left(p\left(\boldsymbol{x}_i;\boldsymbol{\theta}\right)\right)+\log\left(p\left(\boldsymbol{\theta}\right)\right) \end{aligned}$

✍️ תרגיל 3.1 - שיערוך MLE

נתונות $N$ דגימות בלתי תלויות של משתנה אקראי $X$ : $\left\lbrace x_i\right\rbrace_{i=1}^N$ , מצאו את משערך הMLE במקרים הבאים:

א) פילוג נורמלי: $X\sim N\left(\mu,\sigma^2\right)$ עם פרמטרים $\mu$ ו $\sigma^2$ לא ידועים.

ב) פילוג אחיד: $X\sim U\left[0, \theta\right]$ , עם פרמטר $\theta$ לא יודע.

ג) פילוג אקספונציאלי (לקריאה עצמית): $X\sim \exp\left(\theta\right)$ . עם פרמטר $\theta$ לא ידוע.

ד) פילוג דיסקרטי: נתונה קוביה בעלת 6 פאות והסתברות $\left(p_1,\ldots,p_6\right)$ . עם פרמטרים $\left(p_1,\ldots,p_6\right)$ לא ידועים.

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: א) פילוג נורמלי

נסמן $\boldsymbol{\theta}=\left[\theta_1,\theta_2\right]^T=\left[\mu,\sigma^2\right]^T$

על פי הגדרה, משערך הMLE נתון על ידי:

$\begin{aligned} \hat{\boldsymbol{\theta}}_{\text{MLE}} & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \sum_{i=1}^N\log\left(p\left(\boldsymbol{x}_i;\boldsymbol{\theta}\right)\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad \sum_{i=1}^N\log\left(\frac{1}{\sqrt{2\pi\theta_2}}\exp\left(-\frac{1}{2\sigma^2}\left(x_i-\theta_1\right)^2\right)\right) \\ & = \underset{\boldsymbol{\theta}}{\arg\max}\quad -\frac{N}{2}\log\left(2\pi\theta_2\right)-\sum_{i=1}^N\frac{1}{2\theta_2}\left(x_i-\theta_1\right)^2 \\ \end{aligned}$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: א) פילוג נורמלי - המשך

נפתור על ידי גזירה והשוואה ל 0:

$\begin{aligned} & \begin{cases} \frac{\partial}{\partial \theta_1}l\left(\theta\right)=0 \\ \frac{\partial}{\partial \theta_2}l\left(\theta\right)=0 \\ \end{cases} \\ \Leftrightarrow & \begin{cases} \sum_{i=1}^N\frac{1}{\theta_2}\left(x_i-\theta_1\right)=0 \\ -\frac{N}{2\theta_2}+\sum_{i=1}^N\frac{1}{2\theta_2^2}\left(x_i-\theta_1\right)^2=0 \end{cases} \\ \Leftrightarrow & \begin{cases} \theta_1=\frac{1}{N}\sum_{i=1}^N x_i \\ \theta_2=\frac{1}{N}\sum_{i=1}^N\left(x_i-\theta_1\right)^2 \end{cases} \\ \end{aligned}$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: א) פילוג נורמלי - המשך 2

מכאן ש:

$\hat{\mu}_{\text{MLE}}=\hat{\theta}_1=\frac{1}{N}\sum_{i=1}^N x_i \\ \hat{\sigma^2}_{\text{MLE}}=\hat{\theta}_2=\frac{1}{N}\sum_{i=1}^N\left(x_i-\hat{\mu}_{\text{MLE}}\right)^2$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ב) פילוג אחיד

פונקציית צפיפות ההסתברות של הפילוג הנתון הינה:

$p\left(x_i;\theta\right)= \begin{cases} \tfrac{1}{\theta} & \theta\geq x_i\geq 0 \\ 0 & \text{else} \end{cases}$

ולכן:

$\mathcal{L}\left(\theta\right)=p\left(D;\theta\right)=\prod_{i=1}^N p\left(x_i;\theta\right)= \begin{cases} \tfrac{1}{\theta^N} & \forall x_i, x_i\leq\theta \\ 0 & \text{else} \end{cases}$

מכאן ש:

$\hat{\theta}_{\text{MLE}} = \underset{\theta}{\arg\max}\quad \mathcal{L}\left(\theta\right)=\max\left\lbrace x_i\right\rbrace_{i=0}^N$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ג) פילוג אקספוננציאלי

פונקציית צפיפות ההסתברות של הפילוג הנתון הינה:

$p\left(x_i;\theta\right)=\theta\exp\left(-\theta x_i\right)$

ולכן על פי הגדרת משערך הMLE נקבל כי:

$\begin{aligned} \hat{\theta}_{\text{MLE}} & = \underset{\theta}{\arg\max}\quad l\left(\theta\right) \\ & = \underset{\theta}{\arg\max}\quad \sum_{i=1}^N\log\left(p\left(\boldsymbol{x}_i;\boldsymbol{\theta}\right)\right) \\ & = \underset{\theta}{\arg\max}\quad N\log\left(\theta\right)-\theta\sum_{i=1}^N x_i \\ \end{aligned}$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ג) פילוג אקספוננציאלי - המשך

נפתור על ידי גזירה והשוואה ל 0:

$\begin{aligned} & \frac{\partial}{\partial\theta}l\left(\theta\right)=0 \\ \Leftrightarrow & \frac{N}{\theta}-\sum_{i=1}^N x_i=0 \\ \Leftrightarrow & \theta=\frac{1}{\frac{1}{N}\sum_{i=1}^N x_i} \\ \end{aligned}$

מכאן ש:

$\hat{\theta}_{\text{MLE}} = \frac{1}{\frac{1}{N}\sum_{i=1}^N x_i}$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי

נסמן: $\boldsymbol{\theta}=\left[p_1,\ldots,p_6\right]^T$ .

פונקציית ההסתברות של הפילוג הנתון הינה:

$p\left(x\right)=\theta_x$

עלינו להתחשב באילוץ: $\left\lVert\boldsymbol{\theta}\right\rVert_1=\sum_{j=1}^6\theta_j=1$

את משערך הMLE מקבל על ידי פתרון:

$\begin{aligned} \underset{\boldsymbol{\theta}}{\arg\max}\quad & l\left(\boldsymbol{\theta}\right) \\ \text{s.t.} & \left\lVert\boldsymbol{\theta}\right\rVert_1=\sum_{j=1}^6\theta_j=1 \end{aligned}$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי - המשך

נרשום את הLagrangian

$\begin{aligned} L\left(\boldsymbol{\theta},\lambda\right) & = l\left(\boldsymbol{\theta}\right)-\lambda\left(\sum_{j=1}^6\theta_j-1\right) \\ & = \sum_{i=1}^N\log\left(\theta_x\right)-\lambda\left(\sum_{j=1}^6\theta_i-1\right) \\ & = \sum_{j=1}^6\underbrace{\sum_{i=1}^N I\left\lbrace x_i=j\right\rbrace}_{\triangleq m_j}\log\left(\theta_j\right)-\lambda\left(\sum_{j=1}^6\theta_i-1\right) \\ \end{aligned}$

( $\mathcal{L}$ - פונקציית הסבירות, $L$ - Lagrangian)

$m_j$ - מספר הפעמים אשר הערך $j$ מופיע במדגם.

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי - המשך 2

נגזור את הLagrangian לפי הפרמטרים $\boldsymbol{\theta},\lambda$ ונשווה ל-0:

$\begin{aligned} & \begin{cases} \frac{\partial}{\partial\theta_l}\log\left(L\left(\boldsymbol{\theta},\lambda\right)\right)=0\\ \frac{\partial}{\partial\lambda}\log\left(L\left(\boldsymbol{\theta},\lambda\right)\right)=0\\ \end{cases} \\ \Leftrightarrow & \begin{cases} \frac{m_l}{\theta_l}-\lambda=0\\ \sum_{j=1}^6\theta_j-1=0\\ \end{cases} \\ \Leftrightarrow & \begin{cases} \theta_l=\frac{m_l}{\lambda}\\ \sum_{j=1}^6\theta_j=1\\ \end{cases} \\ \Leftrightarrow & \begin{cases} \theta_l=\frac{m_l}{\lambda}\\ \sum_{j=1}^6\frac{m_j}{\lambda}=1\\ \end{cases} \\ \Leftrightarrow & \begin{cases} \theta_l=\frac{m_l}{N}\\ \lambda=\sum_{j=1}^6m_j=N\\ \end{cases} \\ \end{aligned}$

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי - המשך 3

קיבלנו כי

$\hat{p}_{l,\text{MLE}}=\hat{\theta}_l=\frac{m_l}{N}=\frac{1}{N}\sum_{i=1}^N I\left\lbrace x_i=j\right\rbrace$

מקרי הקצה

הטלה בודדת שתוצאתה $x_0$ : $\hat{p}_X\left(x\right)=I\left\lbrace x=x_0\right\rbrace$ .
בגבול $N\rightarrow\infty$ : על פי חוק המספרים הגדולים: $\hat{p}_{l,\text{MLE}}\rightarrow p\left(l\right)=p_l$

✍️ תרגיל 3.2

נתון שהרווח היומי של חברת “רווחילי” מתפלג גאוסית $X\sim N\left(\theta,\sigma_X\right)$ . נתון לנו מדגם אשר מכיל את הרווחים של החברה ב $N$ הימים האחרונים $\left\lbrace x_i\right\rbrace_{i=1}^N$ .

לשם הפשטות נניח שהרווחים בימים שונים הינם בעלי פילוג זהה וכי הם בלתי תלויים סטטיסטית, כלומר הם משתנים i.i.d.

בשאלה זו נניח ש $\sigma_X$ הינו פרמטר ידוע וקבוע ונרצה לחשב את תוחלת הרווח היומי, כלומר לשערך את $\theta$ .

לשם כך, יוסי הציע להשתמש במודל עבור ההתפלגות הפירורית של $\theta$ בהתאם למחקר שביצעו על חברות שונות במשק. יוסי טען שתוחלת הרווח היומי של חברות מתפלגת נורמלי $\theta\sim N\left(\mu_M,\sigma_M\right)$ , עם פרמטרים ידועים $\mu_M$ ו $\sigma_M$ .

א) חשב את משערך הMAP בהתאם למדגם ולפילוג האפריורי שהציע יוסי.

ב) נתחו את תוצאת השיערוך המתקבלת עבור ערכים שונים של $\sigma_X$ ו $\sigma_M$ .

✍️ תרגיל 3.2

💡 פיתרון

נחשב את משערך הMAP על פי הגדרה

$\begin{aligned} & \hat{\mu}_{X,\text{MAP}} \\ & = \underset{\theta}{\arg\max}\quad p\left(\theta\lvert D\right) \\ & = \underset{\theta}{\arg\max}\quad \sum_{i=1}^N\log\left(p\left(x_i\lvert M=\theta\right)\right) + \log\left(p\left(\theta\right)\right) \\ & = \underset{\theta}{\arg\max}\quad \frac{N}{2}\log\left(2\pi\sigma_X^2\right)+\frac{1}{2\sigma_X^2}\sum_{i=1}^N\left(x_i-\theta\right)^2 + \frac{1}{2}\log\left(2\pi\sigma_M^2\right) + \frac{1}{2\sigma_M^2}\left(\theta-\mu_M\right)^2\\ & = \underset{\theta}{\arg\max}\quad \frac{1}{2\sigma_X^2}\sum_{i=1}^N\left(x_i-\theta\right)^2 + \frac{1}{2\sigma_M^2}\left(\theta-\mu_M\right)^2\\ \end{aligned}$

✍️ תרגיל 3.2

💡 פיתרון - המשך

נגזור ונשווה ל-0

$\frac{\partial}{\partial\theta}\left(\frac{1}{2\sigma_X^2}\sum_{i=1}^N\left(x_i-\theta\right)^2 + \frac{1}{2\sigma_M^2}\left(\theta-\mu_M\right)^2\right)=0\\ \Leftrightarrow \frac{1}{\sigma_X^2}\sum_{i=1}^N\left(\theta-x_i\right) + \frac{1}{\sigma_M^2}\left(\theta-\mu_M\right)=0 \\ \Leftrightarrow \theta=\frac{\frac{1}{\sigma_X^2}\sum_{i=1}^Nx_i + \frac{1}{\sigma_M^2}\mu_M}{\frac{N}{\sigma_X^2} + \frac{1}{\sigma_M^2}}$

✍️ תרגיל 3.2

💡 פיתרון - המשך 2

קיבלנו כי:

$\hat{\theta}_{\text{MAP}}=\frac{\frac{1}{\sigma_X^2}\sum_{i=1}^Nx_i + \frac{1}{\sigma_M^2}\mu_M}{\frac{N}{\sigma_X^2} + \frac{1}{\sigma_M^2}}$

נרשום זאת באופן מעט שונה:

$\hat{\theta}_{\text{MAP}}=\frac{\alpha \bar{x} + \beta\mu_M}{\alpha + \beta}$

כאשר:

$\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i\quad, \alpha=\frac{1}{\frac{\sigma_X^2}{N}}\quad, \beta=\frac{1}{\sigma_M^2}$

✍️ תרגיל 3.2

💡 פיתרון - המשך 3

$\hat{\theta}_{\text{MAP}}=\frac{\alpha \bar{x} + \beta\mu_M}{\alpha + \beta}$ $\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i\quad, \alpha=\frac{1}{\frac{\sigma_X^2}{N}}\quad, \beta=\frac{1}{\sigma_M^2}$

נשים לב למספר דברים:

$\bar{x}$ הינו ממוצע הדגימות. זהו הערך אשר ממקסם את פונקציית הסבירות (והוא למעשה משערך הMLE של $\theta$ ).
הערך $\mu_M$ הינו הערך אשר ממקסם את הפילוג האפריורי.
הגודל $\sigma_X^2/N$ הינו השונות של $\bar{x}$ .

התוצאה היא ממוצע מושכלל בין הערך אשר ממקסם את הlikelihood, אשר תלוי במדגם, לבין הערך אשר ממקסם את הפילוג האפריורי.

✍️ תרגיל 3.2

💡 פיתרון - המשך 3

ב) מקרי הקצה.

כאשר $\alpha\gg\beta$ אזי החלק אשר תלוי במדגם מקבל את מרבית המשקל, ומתקיים כי:

$\hat{\mu}_{X,\text{MAP}}\approx\frac{1}{N}\sum_{i=1}^Nx_i$

כאשר $\alpha\ll\beta$ אזי החלק אשר תלוי בפילוג האפריורי מקבל את מרבית המשקל, ומתקיים כי:

$\hat{\mu}_{X,\text{MAP}}\approx\mu_M$

בעיה מעשית

🚖 תזכורת: מדגם נסיעות המונית בNew York

עשרת הדגמים הראשונים במדגם הנסיעות בעיר New York

	passenger_count	trip_distance	payment_type	fare_amount	tip_amount	pickup_easting	pickup_northing	dropoff_easting	dropoff_northing	duration	day_of_week	day_of_month	time_of_day
0	2	2.768065	2	9.5	0.00	586.996941	4512.979705	588.155118	4515.180889	11.516667	3	13	12.801944
1	1	3.218680	2	10.0	0.00	587.151523	4512.923924	584.850489	4512.632082	12.666667	6	16	20.961389
2	1	2.574944	1	7.0	2.49	587.005357	4513.359700	585.434188	4513.174964	5.516667	0	31	20.412778
3	1	0.965604	1	7.5	1.65	586.648975	4511.729212	586.671530	4512.554065	9.883333	1	25	13.031389
4	1	2.462290	1	7.5	1.66	586.967178	4511.894301	585.262474	4511.755477	8.683333	2	5	7.703333
5	5	1.561060	1	7.5	2.20	585.926415	4512.880385	585.168973	4511.540103	9.433333	3	20	20.667222
6	1	2.574944	1	8.0	1.00	586.731409	4515.084445	588.710175	4514.209184	7.950000	5	8	23.841944
7	1	0.804670	2	5.0	0.00	585.344614	4509.712541	585.843967	4509.545089	4.950000	5	29	15.831389
8	1	3.653202	1	10.0	1.10	585.422062	4509.477536	583.671081	4507.735573	11.066667	5	8	2.098333
9	6	1.625433	1	5.5	1.36	587.875433	4514.931073	587.701248	4513.709691	4.216667	3	13	21.783056

❓️ הבעיה: שיעורך הפילוג של משך הנסיעה

אנו מעוניינים לשערך את הפילוג של משך הנסיעה

💡 ניסיון 1: MLE ופילוג גאוסי

שני פרמטרים: התוחלת $\mu$ והשונות $\sigma$ .

סימונים והנחות:

$N$ - מספר הדגמים במדגם.
$\boldsymbol{\theta}=\left[\mu,\sigma\right]^T$ - וקטור הפרמטרים של המודל
$p_\text{normal}\left(x_i;\boldsymbol{\theta}\right)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{\left(x_i-\mu\right)^2}{2\sigma^2}\right), i=1,...,N$ - המודל

במקרה של המודל הנורמלי ניתן לפתור באופן מפורש (אנליטית):

$\mu=\displaystyle{\frac{1}{N}\sum_i x_i} \\ \sigma=\sqrt{\displaystyle{\frac{1}{N}\sum_i\left(x_i-\mu\right)^2}}$

💡 ניסיון 1: MLE ופילוג גאוסי - המשך

בעבור המדגם הנתון נקבל: $\hat{\mu} = 11.4\ \text{min}, \hat{\sigma} = 7.0\ \text{min}$

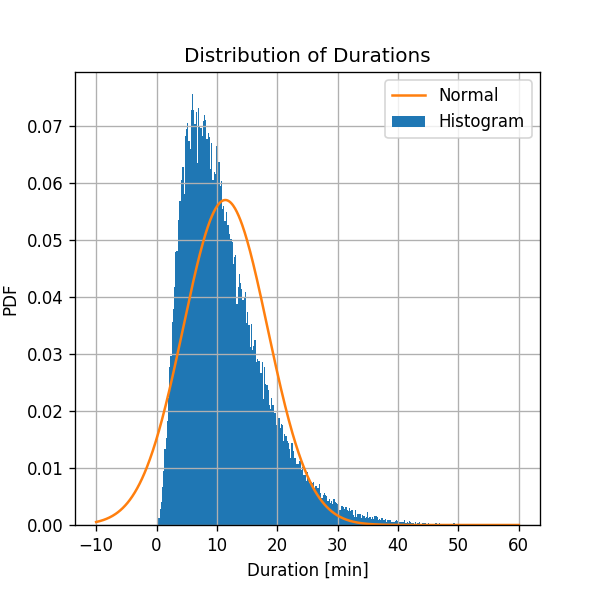
normal

נותן קירוב מאד גס לפילוג האמיתי.
במקרים רבים קירוב זה יהיה מספיק.
ישנו סיכוי לא אפסי לקבל נסיעות עם משך נסיעה שלילי.

ננסה להציע מודל טוב יותר

💡 נסיון 2: MLE ופילוג Rayleigh

בהינתן וקטור גסואי המפולג כך:

$\boldsymbol{Z}\sim N\left(\begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \sigma^2 & 0 \\ 0 & \sigma^2 \end{bmatrix}\right)$

פילוג Rayleigh מתאר את הפילוג של האורך האוקלידי ( $l_2$ norm) של הוקטור:

$\left\lVert\boldsymbol{Z}\right\rVert_2=\sqrt{Z_x^2+Z_y^2}$

פונקציית צפיפות ההסתברות של פילוג Reyligh נתונה על ידי:

$p_\text{Rayleigh}\left(z;\sigma\right)=\frac{z}{\sigma^2}\exp\left({-\frac{z^2}{2\sigma^2}}\right), \quad z\geq0$

מוגדר רק בעבור ערכים חיוביים.
פרמטר יחיד $\sigma$ . (פה $\sigma$ אינה שווה לסטיית התקן של הפילוג).

מוטיבציה לשימוש בפילוג Rayleigh

הנחות:

הוקטור המחבר את נקודת תחילת הנסיעה עם נקודת סיום הנסיעה מפולג נורמלית
רכיביו מפולגים i.i.d.
המונית נוסעת בקירוב בקו ישר בין נקודת ההתחלה והסיום
מהירות הנסיעה קבוע ולכן משך הנסיעה פורפורציוני למרחק.

תחת הנחות אלו נקבל כי:

המרחק אותו נוסעת המכונית יהיה מפולג על פי פילוג Reyleigh וכך גםמשך הנסיעה.

💡 נסיון 2: MLE ופילוג Rayleigh - המשך

נסמן: $\theta=\left[\sigma\right]$

המודל נתון על ידי:

$p_\text{rayleigh}\left(\boldsymbol{x};\theta\right)=\prod_{i=1}^{N}\frac{x_i}{\theta^2}\exp\left(-\frac{x_i^2}{2\theta^2}\right)$

פונקציית ה log likelihood תהיה:

$\begin{aligned} l_\text{rayleigh}\left(\theta\right) & = \sum_i\log\left(p_\text{rayleigh}\left(x_i;\theta\right)\right) \\ & = \sum_i\log\left(x_i\right)-2N\log\left(\theta\right)-\frac{1}{2\theta^2}\sum_ix_i^2 \end{aligned}$

בעיית האופטימיזציה שלנו תהיה:

$\hat{\theta}=\underset{\theta}{\arg\min}\quad-\sum_i\log\left(x_i\right)+2N\log\left(\theta\right)+\frac{1}{2\theta^2}\sum_ix_i^2$

💡 נסיון 2: MLE ופילוג Rayleigh - המשך

$\hat{\theta}=\underset{\theta}{\arg\min}\quad-\sum_i\log\left(x_i\right)+2N\log\left(\theta\right)+\frac{1}{2\theta^2}\sum_ix_i^2$

גם בעבור המקרה הזה נוכל לפתור את בעיית האופטימיזציה באופן אנליטי על ידי גזירה והשוואה לאפס:

$\frac{\partial l_\text{rayleigh}\left(\theta\right)}{\partial\theta}=0 \\ \Leftrightarrow -\frac{2N}{\theta}+\frac{\sum_ix^2}{\theta^3}=0 \\ \Leftrightarrow \hat{\sigma} = \theta = \sqrt{\frac{1}{2N}\sum_i x^2}$

💡 נסיון 2: MLE ופילוג Rayleigh - המשך 2

בעבור המדגם הנתון נקבל: $\hat{\sigma} = 9.5$

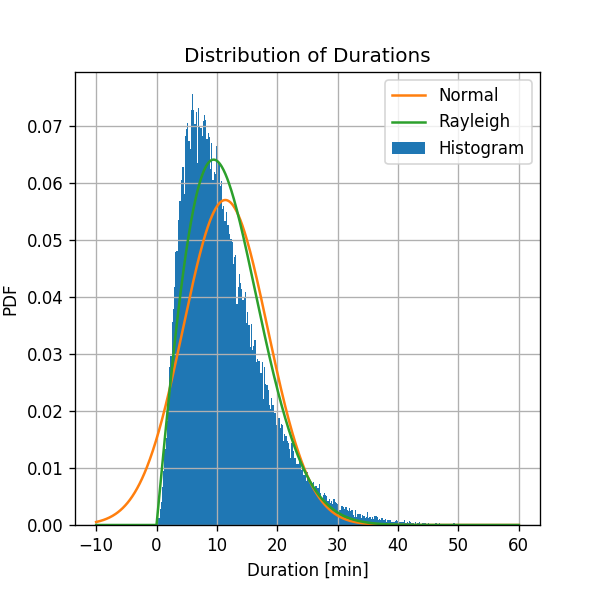
rayleigh

נותן תוצאה מעט יותר טובה מהמודל הנורמלי
אין הסתברות שונה מ0 לקבל משך נסיעה שלילי.

ננסה מודל נוסף.

💡נסיון 3: MLE ו Generalized Gamma Distribution

פילוג Rayleigh הינו מקרה פרטי של Generalized Gamma Distribution:

$p_\text{gengamma}\left(z;\sigma,a,c\right)= \frac{cz^{ca-1}\exp\left(-\left(z/\sigma\right)^c\right)}{\sigma^{ca-1}\Gamma\left(a\right)} , \quad z\geq0$

( $\Gamma$ היא פונקציה המוכנה פונקציית גמא (gamma function) )

למודל זה 3 פרמטרים: $\boldsymbol{\theta}=\left[\sigma, a, c\right]^T$ .

בעבור $c=2$ ו $a=1$ נקבל את פילוג Rayleight כאשר $\sigma_{gamma}=2\sigma_{rayleigh}$ .

💡נסיון 3: MLE ו Generalized Gamma Distribution - המשך

לא נוכל לפתרון בעיה זו באופן אנליטי, נאלץ להעזר פתרון נומרי.

נשתמש באובייקט הGeneralized Gamma Distribution של SciPy.

💡נסיון 3: MLE ו Generalized Gamma Distribution - המשך

קיבלנו: $\hat{a} = 4.4, \hat{c} = 0.8, \hat{\sigma} = 1.6$

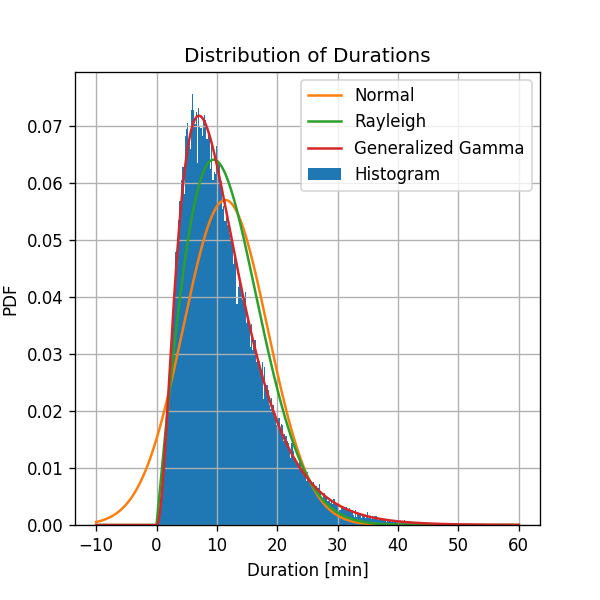
generalized_gamma

Generalized Gamma Distribution מניב תוצאה דומה מאד לצורת ההסטוגרמה.

✍️ תרגיל 3.3: תרגיל ממבחן - אביב 2019, מועד ב’ שאלה 3

נתונות לנו $N$ מדידות IID, $\left\lbrace x_i\right\rbrace_{i=1}^N$ כאשר $x_i$ מגיע מההתפלגות הבאה:

$p\left(x\right)=\frac{1}{\mu}e^{-\frac{1}{\mu}\left(x-\theta\right)}\qquad x\geq\theta,\mu>0$

א) מצאו את משערך הMLE עבור הפרמטר $\mu$ בהנחה כי $\theta$ פרמטר ידוע

ב) מצאו את משערך הMLE עבור הפרמטר $\theta$ בהנחה כי $\mu$ פרמטר ידוע

✍️ תרגיל 3.3: תרגיל ממבחן - אביב 2019, מועד ב’ שאלה 3

$p\left(x\right)=\frac{1}{\mu}e^{-\frac{1}{\mu}\left(x-\theta\right)}I\left\lbrace x\geq\theta\right\rbrace\qquad \mu>0$

💡 פתרון: א

$L\left(\mu\right)=\prod_{i=1}^N\frac{1}{\mu}e^{-\frac{1}{\mu}\left(x_i-\theta\right)}=\frac{1}{\mu^N}e^{-\frac{1}{\mu}\sum_{i=1}^N\left(x_i-\theta\right)}$

תחת התנאי כי $\mu>0$ .

פונקציית הlog-likelihood הינה:

$l\left(\mu\right)=\log\left(L\left(\mu\right)\right)=-N\log\left(\mu\right)-\frac{1}{\mu}\sum_{i=1}^N\left(x-\theta\right)$

מגזירה והשוואה לאפס נקבל:

$\frac{\partial}{\partial\mu}l\left(\mu\right)=-\frac{N}{\mu}+\frac{1}{\mu^2}\sum_{i=1}^N\left(x_i-\theta\right)=0 \\ \Rightarrow \hat{\mu}_{\text{MLE}}=\frac{1}{N}\sum_{i=1}^N\left(x_i-\theta\right)=0$

הנגזרת השנייה שלילית ולכן זוהי אכן נקודת מקסימום.

✍️ תרגיל 3.3: תרגיל ממבחן - אביב 2019, מועד ב’ שאלה 3

$p\left(x\right)=\frac{1}{\mu}e^{-\frac{1}{\mu}\left(x-\theta\right)}\qquad x\geq\theta,\mu>0$

💡 פתרון: ב

נכתוב את ה-likelihood:

$L\left(\theta\right)\prod_{i=1}^N\frac{1}{\mu}e^{-\frac{1}{\mu}\left(x_i-\theta\right)}I\left\lbrace x_i\geq\theta\right\rbrace=\frac{1}{\mu^N}e^{-\frac{1}{\mu}\sum_{i=1}^N\left(x_i-\theta\right)}I\left\lbrace \min\left\lbrace x_i\right\rbrace\geq\theta\right\rbrace$

נשים לב כי $L\left(\theta\right)$ היא פונקציה מונוטונית עולה ב $\theta$ בתחום שבו $\min\left\lbrace x_i\right\rbrace\geq\theta$ . לכן שמערך הסבירות המירבית יתקבל בערך המקסימאלי האפשרי עבור $\theta$ בתחום זה: $\hat{\theta}_{\text{MLE}}=\min\left\lbrace x_i\right\rbrace$ .

תרגול 3שיערוך פילוג בשיטות פרמטריות

תיאוריה

המטרה

הגישה הפרמטרית והלא פרמטרית

הבעיה בגישה הלא פרמטרית

הגישה הפרמטרית

המטרה

הגישה באייסיאנית והלא-בייסיאנית

הגישה באייסיאנית

הפילוג p\left(\boldsymbol{\theta}\right):

הפילוג p\left(\boldsymbol{\theta}\lvert D\right):

הגישה באייסיאנית והלא-בייסיאנית

הגישה הלא-בייסיאנית (המכונה גם: קלאסית או תדירותית (Frequintist))

שיטות שיערוך

משערך (Maximum a Posteriori (MAP (שיטה בייסיאנית)

שיטות שיערוך

משערך (Maximum a Posteriori (MAP (שיטה בייסיאנית) - המשך

שיטות שיערוך

משערך Maximum Likelihood Estimator (MLE) (שיטה לא בייסיאנית)

הlog-likelihood והנחת הIID

הlog-likelihood והנחת הIID - המשך

הlog-likelihood והנחת הIID - המשך 2

✍️ תרגיל 3.1 - שיערוך MLE

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: א) פילוג נורמלי

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: א) פילוג נורמלי - המשך

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: א) פילוג נורמלי - המשך 2

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ב) פילוג אחיד

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ג) פילוג אקספוננציאלי

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ג) פילוג אקספוננציאלי - המשך

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי - המשך

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי - המשך 2

✍️ תרגיל 3.1 - שיערוך MLE

💡 פיתרון: ד) פילוג דיסקרטי - המשך 3

מקרי הקצה

✍️ תרגיל 3.2

✍️ תרגיל 3.2

💡 פיתרון

✍️ תרגיל 3.2

💡 פיתרון - המשך

✍️ תרגיל 3.2

💡 פיתרון - המשך 2

✍️ תרגיל 3.2

💡 פיתרון - המשך 3

✍️ תרגיל 3.2

💡 פיתרון - המשך 3

בעיה מעשית

🚖 תזכורת: מדגם נסיעות המונית בNew York

❓️ הבעיה: שיעורך הפילוג של משך הנסיעה

💡 ניסיון 1: MLE ופילוג גאוסי

💡 ניסיון 1: MLE ופילוג גאוסי - המשך

💡 נסיון 2: MLE ופילוג Rayleigh

מוטיבציה לשימוש בפילוג Rayleigh

💡 נסיון 2: MLE ופילוג Rayleigh - המשך

💡 נסיון 2: MLE ופילוג Rayleigh - המשך

💡 נסיון 2: MLE ופילוג Rayleigh - המשך 2

💡נסיון 3: MLE ו Generalized Gamma Distribution

💡נסיון 3: MLE ו Generalized Gamma Distribution - המשך

💡נסיון 3: MLE ו Generalized Gamma Distribution - המשך

✍️ תרגיל 3.3: תרגיל ממבחן - אביב 2019, מועד ב’ שאלה 3

✍️ תרגיל 3.3: תרגיל ממבחן - אביב 2019, מועד ב’ שאלה 3

💡 פתרון: א

✍️ תרגיל 3.3: תרגיל ממבחן - אביב 2019, מועד ב’ שאלה 3

💡 פתרון: ב

תרגול 3
שיערוך פילוג בשיטות פרמטריות

הפילוג $p\left(\boldsymbol{\theta}\right)$ :

הפילוג $p\left(\boldsymbol{\theta}\lvert D\right)$ :